
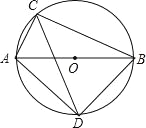
【题目】如图所示,⊙O的直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于点D,
(1)求证:△ABD是等腰三角形;
(2)求CD的长.
【答案】(1)详见解析;(2)CD=7![]() .
.
【解析】
(1)连接OD,根据角平分线的定义得到∠ACD=∠BCD,根据圆周角定理,等腰三角形的定义证明即可;
(2)作AE⊥CD于E,根据等腰直角三角形的性质求出AD,根据勾股定理求出AE、CE,DE,结合图形计算,即可得到答案.
(1)连接OD.
∵AB为⊙O的直径,∴∠ACB=90°.
∵CD是∠ACB的平分线,∴∠ACD=∠BCD=45°,由圆周角定理得:∠AOD=2∠ACD=90°,∠BOD=2∠BCD=90°,∴∠AOD=∠BOD=90°,∴DA=DB,即△ABD是等腰三角形;
(2)作AE⊥CD于E.
∵AB为⊙O的直径,∴∠ADB=90°,∴AD![]() AB=5
AB=5![]() .
.
∵AE⊥CD,∠ACE=45°,∴AE=CE=![]() AC=3
AC=3![]() .在Rt△AED中,DE
.在Rt△AED中,DE![]() ,∴CD=CE+DE=3
,∴CD=CE+DE=3![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径 ,点C在⊙O上,过点O作![]() 交BC于点E,交⊙O于点D,CD∥AB.
交BC于点E,交⊙O于点D,CD∥AB.
(1)求证:E为OD的中点;
(2)若CB=6,求四边形CAOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(0,2),B(2,﹣2)两点.
⑴用含a的式子表示b.
⑵当a=﹣![]() 时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
⑶若a>0,线段AB下方的抛物线上有一点E,求证:不管a取何值,当△EAB的面积最大时,E点的横坐标为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
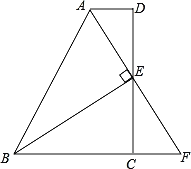
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以PQCD为顶点的四边形是平行四边形是否存在?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,为了躲避台风,一轮船一直由西向东航行,上午![]() 点,在
点,在![]() 处测得小岛
处测得小岛![]() 的方向是北偏东
的方向是北偏东![]() ,以每小时
,以每小时![]() 海里的速度继续向东航行,中午
海里的速度继续向东航行,中午![]() 点到达
点到达![]() 处,并测得小岛
处,并测得小岛![]() 的方向是北偏东
的方向是北偏东![]() ,若小岛周围
,若小岛周围![]() 海里内有暗礁,问该轮船是否能一直向东航行?
海里内有暗礁,问该轮船是否能一直向东航行?

查看答案和解析>>
科目:初中数学 来源: 题型:
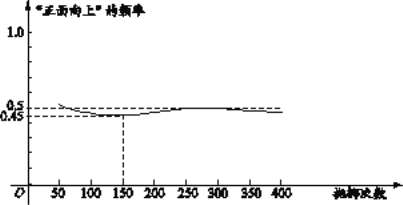
【题目】下图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com