
科目:初中数学 来源: 题型:解答题
 某人带自产的土豆进城出售,他先按市场价售出一些后,发现天色较晚,决定降价出售.为了方便顾客,他的钱包中有一些备用零钱用于找零.学习小组观察发现售出土豆数量x与他钱包中的总钱数y的关系如图所示.结合图象回答下列问题:
某人带自产的土豆进城出售,他先按市场价售出一些后,发现天色较晚,决定降价出售.为了方便顾客,他的钱包中有一些备用零钱用于找零.学习小组观察发现售出土豆数量x与他钱包中的总钱数y的关系如图所示.结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
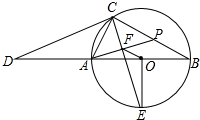
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.设AP=x.当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式及定义域.
如图,将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.设AP=x.当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式及定义域.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com