
分析 直接利用绝对值的性质得出:|x+l|+|x-2|≥3,|y-2|+|y+1|≥3,|z-3|+|z+l|≥4,进而利用已知得出答案.
解答 解:∵|x+l|+|x-2|≥3,
|y-2|+|y+1|≥3,
|z-3|+|z+l|≥4,
∴(|x+l|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+l|)≥36,
∵(|x+l|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+l|)=36,
∴|x+l|+|x-2|=3,|y-2|+|y+1|=3,|z-3|+|z+l|=4,
∴-1≤x≤2,-1≤y≤2,-2≤z≤3,
∴-1≤x≤2,-2≤2y≤4,-6≤3z≤9,
∴-9≤x+2y+3z≤15,
故最大值15,最小值-9.
点评 此题主要考查了绝对值,正确得出x,y,z的取值范围是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
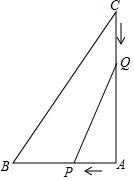 如图,在△ABC中,已知∠BAC=90°,AB=6cm,AC=8cm,点P从点A出发以1cm/s的速度移动到点B,点Q从点C出发以2cm/s的速度移动到点A.
如图,在△ABC中,已知∠BAC=90°,AB=6cm,AC=8cm,点P从点A出发以1cm/s的速度移动到点B,点Q从点C出发以2cm/s的速度移动到点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com