
【题目】如图,等边△DEF的顶点在等边△ABC的边上.

(1)求证:BE=CD;
(2)若BD=2CD,求∠DFC的度数.
【答案】(1)见解析;(2)∠FDC=90°
【解析】
(1)欲证明BE=CD,只要证明△BDE≌△CFD(AAS)即可;
(2)取BD的中点M,连接EM.首先证明△BEM是等边三角形,由EM=BM=DM推出∠DEB=90°,求出∠BDE即可解决问题;
(1)证明:∵△ABC,△DEF都是等边三角形,
∴∠B=∠C=∠EDF=60°,DE=DF,
∵∠EDC=∠B+∠BED=∠EDF+∠CDF,
∴∠BED=∠CDF,
∴△BDE≌△CFD(AAS),
∴BE=CD.
(2)解:取BD的中点M,连接EM.
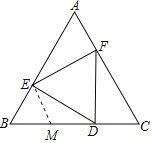
∵BD=2CD,BE=CD,
∴BD=2BE,
∵BM=MD,
∴BE=BM,
∵∠B=60°,
∴△BME是等边三角形,
∴EM=BM=MD,
∴∠BED=90°,
∴∠EDB=30°,
∴∠FDC=180°﹣30°﹣60°=90°.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.例:已知![]() ,则点
,则点![]() 为
为![]() 的准外心(如图
的准外心(如图![]() ).
).
![]() 如图
如图![]() ,
,![]() 为正三角形
为正三角形![]() 的高,准外心
的高,准外心![]() 在高
在高![]() 上,且
上,且![]() ,求
,求![]() 的度数.
的度数.
![]() 如图
如图![]() ,若
,若![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,
,![]() ,准外心
,准外心![]() 在
在![]() 边上,试探究
边上,试探究![]() 的长.
的长.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的解析式是![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 抛物线的对称轴是直线![]() B. 抛物线的顶点坐标是
B. 抛物线的顶点坐标是![]() C. 该二次函数有最小值
C. 该二次函数有最小值![]() D. 当
D. 当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() 的
的![]() 、
、![]() 两个顶点在
两个顶点在![]() 轴上,顶点
轴上,顶点![]() 在
在![]() 轴的负半轴上.已知
轴的负半轴上.已知![]() ,
,![]() ,
,![]() 的面积
的面积![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 、
、![]() 三点.
三点.

![]() 求此抛物线的函数表达式;
求此抛物线的函数表达式;
![]() 点
点![]() 是抛物线对称轴上的一点,在线段
是抛物线对称轴上的一点,在线段![]() 上有一动点
上有一动点![]() ,以每秒
,以每秒![]() 个单位的速度从
个单位的速度从![]() 向
向![]() 运动,(不与点
运动,(不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,试把
秒,试把![]() 的面积
的面积![]() 表示成
表示成![]() 的函数,当
的函数,当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值;
有最大值,并求出最大值;
![]() 设点
设点![]() 是抛物线上异于点
是抛物线上异于点![]() ,
,![]() 的一个动点,过点
的一个动点,过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() .以
.以![]() 为直径画
为直径画![]() ,则在点
,则在点![]() 的运动过程中,是否存在与
的运动过程中,是否存在与![]() 轴相切的
轴相切的![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
①写出图中一对全等的三角形,并写出它们的所有对应角;
②设![]() 的度数为x,∠
的度数为x,∠![]() 的度数为
的度数为![]() ,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.
(2)如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com