
��ͼ��1�������ı���ABCD�У���֪��ABC ��ADC
��ADC 180�㣬AB
180�㣬AB AD��AB
AD��AB AD����E��CD���ӳ����ϣ���1
AD����E��CD���ӳ����ϣ���1 ��2��
��2��
��1����֤����3 ��E��
��E��
��2����֤��CAƽ�֡�BCD��
��3����ͼ��2������AF�ǡ�ABC�ı�BC�ϵĸߣ���֤��CE 2AF��
2AF��

 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㶫ʡ��ݸ�к���ѧУ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ���word�溬�𰸽����� ���ͣ���ѡ��
��A����3��2������y��ԳƵĵ������Ϊ��������
A. ��3����2�� B. ��3��2�� C. ����3����2�� D. ��2����3��
B ���������������� A����3��2������y��ԳƵĵ������Ϊ��3��2������ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ����ʮ���´����� ���ͣ���ѡ��
��ֱ��y=2x����ƽ��2����λ���õ�ֱ�ߵĽ���ʽ�ǣ�������
A. y=2x+2 B. y=2x��2 C. y=2��x��2�� D. y=2��x+2��
C ����������ֱ֪��y=2x����ƽ��2����λ�����ݶ�Ӧ��������겻�䣬�������2���ɵ��µĽ���ʽ��y=2��x��2������ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ������
��ͼ��ʾ���ڵ���������ABC�У�tan A��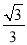 ��AB��BC��8����AB���ϵĸ�CD�ij���__��
��AB��BC��8����AB���ϵĸ�CD�ij���__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ���ڶ�ʮ���� ������ ���ͣ���ѡ��
��ͼ����ƽ��ֱ������ϵ�У�P�ǵ�һ�����ڵĵ㣬��������(3��m)����OP��x��������ļнǦ�������ֵ�� ����sin����ֵ��(����)
����sin����ֵ��(����)

A. 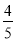 B.
B.  C.
C.  D.
D. 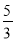
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ܿ���������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ�

��1����֪��B=30�㣬��C=60�㣬���DAE�Ķ�����
��2�����B= x����C= y��x < y������ֱ��д����DAE�Ķ��� �����ú�x ��y�Ĵ���ʽ��ʾ��
��1����EAD=15��;(2) ��EAD= (y-x) ����������������������1�������������ڽǺͶ��������BAC���ٸ��ݽ�ƽ���ߵĶ��������EAC������ֱ������������ǻ��������DAC��Ȼ����⼴�ɣ���2��ͬ��1�����ɵó������ ��������� ��1�� �� �� ��AEƽ��, �� �� ��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�ܿ���������2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
���㣺  _________________��
_________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ��ʦ����ϲ� ��1�� �ḻ��ͼ������ ��Ԫ���Ծ� ���ͣ������
�����������������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����A��B��C��D��EΪ��O����ȷֵ㣬����M��Բ��O���������߶�OA���ӻ�AC���߶�CO��·���������˶������˶���ʱ��Ϊt����DME�Ķ���Ϊy��������ͼ���б�ʾy��t֮�亯����ϵ��ǡ�����ǣ� ��

A. 
B. 
C. 
D. 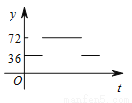
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com