
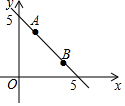
 如图,已知一次函数y=mx+5的图象经过点A(1,4)、B(n,2).
如图,已知一次函数y=mx+5的图象经过点A(1,4)、B(n,2).分析 (1)根据点A的坐标利用待定系数法可求出m值,进而可得出一次函数解析式,再利用一次函数图象上点的坐标特征即可求出n值;
(2)利用一次函数图象上点的坐标特征可求出直线AB与x轴的交点坐标,观察函数图象,即可得出当函数图象在第一象限时,自变量x的取值范围;
(3)作点A关于x轴的对称点A′,连接A′B交x轴于点P,此时点P为所求的点,由点A的坐标可得出点A′的坐标,根据点A′、B的坐标利用待定系数法可求出直线A′B的解析式,再利用一次函数图象上点的坐标特征即可求出点P的坐标.
解答 解:(1)∵一次函数y=mx+5的图象经过点A(1,4),
∴m+5=4,解得:m=-1;
∵点B在一次函数y=-x+5的图象上,
∴-n+5=2,解得:n=3.
∴m、n的值分别是-1、3.
(2)当y=-x+5=0时,x=5,
∴一次函数y=-x+5的图象与x轴的交点坐标为(5,0).
观察函数图象可知:当0<x<5时,一次函数y=-x+5的图象在第一象限,
∴当函数图象在第一象限时,自变量x的取值范围是0<x<5.
(3)作点A关于x轴的对称点A′,连接A′B交x轴于点P,此时点P为所求的点,如图所示.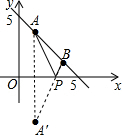
∵点A(1,4),
∴A′(1,-4).
设直线A′B的解析式为y=kx+b,
将A′(1,-4)、B(3,2)代入y=kx+b,
$\left\{\begin{array}{l}{k+b=-4}\\{3k+b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=3}\\{b=-7}\end{array}\right.$,
∴直线A′B的解析式为y=3x-7.
当y=3x-7=0时,x=$\frac{7}{3}$,
∴点P的坐标为($\frac{7}{3}$,0).
点评 本题考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及轴对称中的最短路线问题,解题的关键是:(1)由点A的坐标利于待定系数法求出直线AB的解析式;(2)利于一次函数图象上点的坐标特征求出直线AB与x轴的交点坐标;(3)根据两点之间线段最短,找出点P的位置.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
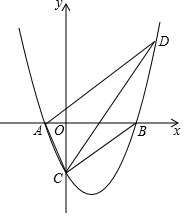 已知抛物线y=ax2+bx-3a与x轴交于A(-1,0),B(x2,0),与y轴负半轴交于点C,OB=OC.
已知抛物线y=ax2+bx-3a与x轴交于A(-1,0),B(x2,0),与y轴负半轴交于点C,OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,4) | B. | (-3,1) | C. | (0,-2) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查乘坐飞机的旅客是否携带了违禁物品 | |
| B. | 调查2017年央视春晚的全国收视率 | |
| C. | 调查某品牌日光灯的使用寿命 | |
| D. | 调查市场上营养快线的质量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com