
【题目】已知:如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于点D,经过B、D两点的⊙O交AB 于点E,交BC于点F,EB为⊙O的直径. 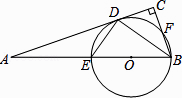
(1)求证:AC是⊙O的切线;
(2)当BC=2,cos∠ABC= ![]() 时,求⊙O的半径.
时,求⊙O的半径.
【答案】
(1)证明:如图,连结OD.
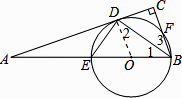
∴OD=OB.
∴∠1=∠2.
∵BD平分∠ABC,
∴∠1=∠3.
∴∠2=∠3.
∴OD∥BC.
∴∠ADO=∠C=90°.
∴OD⊥AC.
∵OD是⊙O的半径,
∴AC是⊙O的切线
(2)解:在Rt△ACB中,∠C=90,BC=2,cos∠ABC= ![]() ,
,
∴ ![]() .
.
设⊙O的半径为r,则AO=6﹣r.
∵OD∥BC,
∴△AOD∽△ABC.
∴ ![]() .
.
∴ ![]() .
.
解得 ![]() .
.
∴⊙O的半径为 ![]()
【解析】(1)根据切线的判定定理,垂直经过半径外端的直线是圆的切线,连接OD,只要得出OD⊥AC即可得出;(2)通过解直角三角形求得AB,然后证明△AOD∽△ABC,利用相似的性质得对应边的比值相等,即可求得⊙O的半径.
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上. 
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
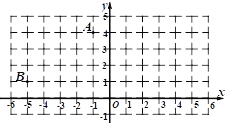
【题目】点A(1,4)和点B(5,1)在平面直角坐标系中的位置如图所示:
(1)点A1、B1分别为点A、B关于y轴的对称点,请画出四边形AA1B1B,并写出A1、B1的坐标;
(2)在(1)的条件下,画一条过四边形AA1B1B的一个顶点的线段,将四边形AA1B1B分成两个图形,并且使分得的图形中的一个是轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝元旦,某校组织大合唱汇演.初一(1)、(2)班学生准备统一购买服装参加演出(一人买一套),这两班共有学生104名学生参加演出,其中(1)班人数较少,不足50人.下面是某服装厂给出的服装价格表:
购买服装的套数 | 1﹣50套 | 51﹣100套 | 100套以上 |
每套服装的价格 | 130元 | 110元 | 90元 |
经估算,如果两个班都以班为单位购买服装,那么一共应付12400元,问:
(1)两班各有多少学生?
(2)如果两班联合起来,作为一个团体购买服装,可省多少钱?
(3)如果(2)班不购买了,只有(1)班单独购买,作为组织者的你将如何购买才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
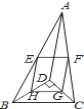
A. 7 B. 8 C. 11 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举办“体彩杯”中学生篮球赛,初中男子组有市直学校的A、B、C三个队和县区学校的D,E,F,G,H五个队,如果从A,B,D,E四个队与C,F,G,H四个队中个抽取一个队进行首场比赛,那么首场比赛出场的两个队都是县区学校队的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(﹣1,0),(5,0),(0,2).若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P在移动的过程中,使△PBF成为直角三角形,则点F的坐标是 . 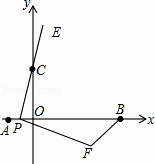
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com