
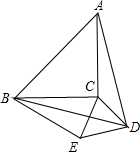
 如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边作等边△DCE.B、E在C、D的同侧,若AB=
如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边作等边△DCE.B、E在C、D的同侧,若AB=| 2 |
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
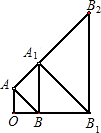 如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第2008个等腰直角三角形的面积S2008=
如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,…,如此作下去,若OA=OB=1,则第2008个等腰直角三角形的面积S2008=查看答案和解析>>
科目:初中数学 来源:《第23章 旋转》2012年单元综合训练卷(西城区)(解析版) 题型:填空题
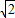 ,则BE= .
,则BE= .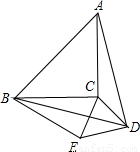
查看答案和解析>>
科目:初中数学 来源:初三数学圆及旋转题库 第1讲:旋转1(解析版) 题型:填空题
 ,则BE= .
,则BE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com