
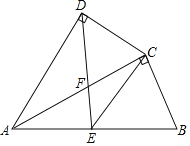
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD.
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求AF的值.
【答案】(1)详见解析;(2)详见解析;(3)AF=![]() .
.
【解析】
(1)先根据角平分线得出∠CAD=∠CAB,进而判断出△ADC∽△ACB,即可得出结论;
(2)先利用直角三角形的性质得出CE=AE,进而得出∠ACE=∠CAE,从而∠CAD=∠ACE,即可得出结论;
(3)由(1)的结论求出AC,再求出CE=3,最后由(2)的结论得出△CFE∽△AFD,即可得出结论.
解:(1)∵AC平分∠BAD,
∴∠CAD=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴![]() ,
,
∴AC2=ADAB;
(2)在Rt△ABC中,∵E为AB的中点,
∴CE=AE(直角三角形斜边的中线等于斜边的一半),
∴∠ACE=∠CAE,
∵AC平分∠BAD,
∴∠CAD=∠CAE,
∴∠CAD=∠ACE,
∴CE∥AE;
(3)由(1)知,AC2=ADAB,
∵AD=4,AB=6,
∴AC2=4×6=24,
∴AC=2![]() ,
,
在Rt△ABC中,∵E为AB的中点,
∴CE=![]() AB=3,
AB=3,
由(2)知,CE∥AD,
∴△CFE∽△AFD,
∴![]() ,
,
∴![]() ,
,
∴AF=![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
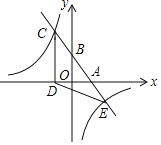
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
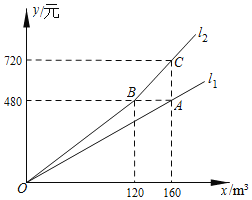
【题目】某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中![]() 、
、![]() 分别表示去年、今年水费
分别表示去年、今年水费![]() (元)与用水量
(元)与用水量![]() (
(![]() )之间的关系.小雨家去年用水量为150
)之间的关系.小雨家去年用水量为150![]() ,若今年用水量与去年相同,水费将比去年多_____元.
,若今年用水量与去年相同,水费将比去年多_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
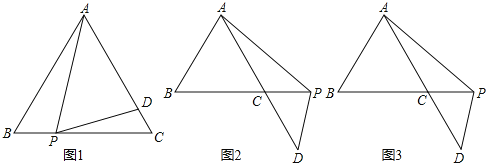
【题目】已知等边△ABC的边长为2,
(1)如图1,在边BC上有一个动点P,在边AC上有一个动点D,满足∠APD=60°,求证:△ABP~△PCD
(2)如图2,若点P在射线BC上运动,点D在直线AC上,满足∠APD=120°,当PC=1时,求AD的长
(3)在(2)的条件下,将点D绕点C逆时针旋转120°到点D',如图3,求△D′AP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A.C的坐标和△AOC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com