Question

16．如图，在平面直角坐标系中，?OABC的OA边在x轴正半轴上，点C，B在第一象限内，∠AOC=60°，A（4，0），OC=2
（1）求B点坐标；
（2）点P是x轴上一动点，当点P在什么位置时，线段CP与线段BP之和最短？请在图中标出点P，并求出此时点P的坐标和CP+BP的值．

Answer 1

分析 （1）过C作CE⊥OA，过B作BF⊥OA，先利用三角函数求出OE、CE的长度，从而得出C点纵坐标坐标，然后利用平行四边形的性质求得点B的坐标，；
（2）作点C关于x轴的对称点C′，连接C′B交x轴于P，则此时线段CP与线段BP之和最短，即CP+BP=C′B，根据勾股定理得到BC′=$\sqrt{（2\sqrt{3}）^{2}+{4}^{2}}$=2$\sqrt{7}$．于是得到CP+BP的最短距离是2$\sqrt{7}$，由于OE=1，PE=$\frac{1}{2}$BC=2，得到OP=1+2=3，即可得到结论．

解答 解：（1）如图1，过C作CE⊥OA，过B作BF⊥OA，
由题意可得OA=4，∠AOC=60°，
∴OE=1，CE=$\sqrt{3}$，
∵四边形OABC是平行四边形，
∴BC∥OA，
∴B和C的纵坐标相等，
∴B的纵坐标为$\sqrt{3}$，
∵AF=1，
∵OA=4，
∴OF=5，
∴点B的横坐标坐标是5，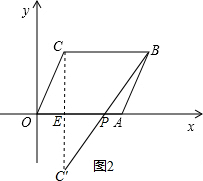
∴点B的坐标是（5，$\sqrt{3}$）；

（2）如图2，作点C关于x轴的对称点C′，
连接C′B交x轴于P，则此时线段CP与线段BP之和最短，
即CP+BP=C′B，
∵BC∥OA，
∴∠BCC′=90°，CC′=2$\sqrt{3}$，BC=OA=4，
∴BC′=$\sqrt{（2\sqrt{3}）^{2}+{4}^{2}}$=2$\sqrt{7}$．
∴CP+BP的最短距离是2$\sqrt{7}$，
∵OE=1，PE=$\frac{1}{2}$BC=2，
∴OP=1+2=3，
∴P（3，0）．

点评 本题考查了轴对称-最短距离问题，平行四边形的性质，勾股定理，坐标与图形的性质，正确的作出图形是解题的关键．