
 菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24.
菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24. 分析 连接BD,交AC于O,根据菱形的两条对角线互相垂直且平分可得AO=CO=$\frac{1}{2}$AC=4,BO=DO,CA⊥BD,然后利用勾股定理计算出BO的长,进而可得BD长,再利用菱形的面积公式进行计算即可.
解答 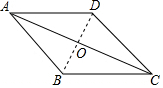 解:连接BD,交AC于O,
解:连接BD,交AC于O,
∵四边形ABCD是菱形,
∴AO=CO=$\frac{1}{2}$AC=4,BO=DO,CA⊥BD,
∵AB=5,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=3,
∴BD=6,
∴菱形ABCD的面积为:$\frac{1}{2}×$6×8=24,
故答案为:24.
点评 此题主要考查了菱形的性质,关键是掌握菱形的两条对角线互相垂直且平分.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 50 | 80 | 100 | 120 |
| y | 40 | 34 | 30 | 26 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2-3=8 | B. | -2-3=$\frac{1}{8}$ | C. | -2-3=-$\frac{1}{8}$ | D. | (2017-π)0=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
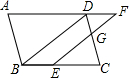 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )| A. | $\frac{25a}{8}$ | B. | $\frac{25a}{9}$ | C. | $\frac{25a}{16}$ | D. | $\frac{16a}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
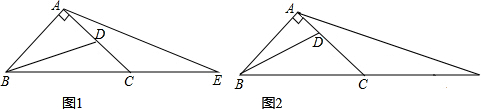
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
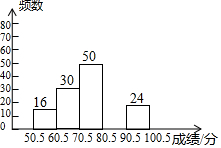 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5-60.5 | 16 | 0.08 |
| 二 | 60.5-70.5 | 30 | 0.15 |
| 三 | 70.5-80.5 | 50 | 0.25 |
| 四 | 80.5-90.5 | m | 0.40 |
| 五 | 90.5-100.5 | 24 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com