
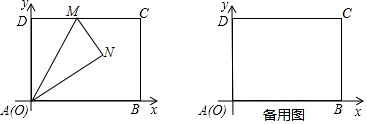
���� ��1�����۵������ʵã���ANM�ա�ADM���ɽ�ƽ���߽�ϵã���BAM=��MAN=��NAB=30�㣬������ǵ����Ǻ�������DM�ij���д��M�����ꣻ
��2����ͼ2���������ߣ�����ֱ�������Σ���NQ=x����AQ=MQ=1+x����Rt��ANQ�У��ɹ��ɶ����е�ʽ�ɵù���x�ķ��̣���x+1��2=32+x2�����x���ó�AB��AQ��$\frac{4}{5}$�����ɵó���NAQ�͡�NAB�Ĺ�ϵ���ó����ۣ�
��III����ͼ3����A��AH��BF��H��֤����ABH�ס�BFC����$\frac{BH}{AH}=\frac{CF}{BC}$��Rt��AHN�У���AH��AN=3��AB=4����֪������N��H�غϣ���AH=AN��ʱ��AH���BH��С��CF��С��DF���ʱ��M��F�غϣ�B��N��M���㹲�ߣ���ͼ4��ʾ�����ʱDF�ij����ɣ�
��� 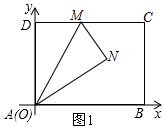 �⣺��I����A��0��0����B��4��0����D��0��3����
�⣺��I����A��0��0����B��4��0����D��0��3����
��AD=3��AB=4��
���۵��ã���ANM�ա�ADM��
���MAN=��DAM��
��ANƽ�֡�MAB��
���MAN=��NAB��
���BAM=��MAN=��NAB��
���ı���ABCD�Ǿ��Σ�
���DAB=90�㣬
���DAM=30�㣬
��DM=AD•tan��DAM=3��tan30��=3��$\frac{\sqrt{3}}{3}$=$\sqrt{3}$��
���DAM=30�㣬M��$\sqrt{3}$��3����
��II���ӳ�MN��AB���ӳ����ڵ�Q��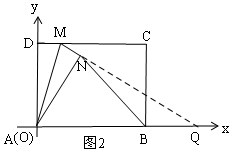
���ı���ABCD�Ǿ��Σ�
��AB��CD��
���DMA=��MAQ��
���۵��ã���ANM�ա�ADM��
���DMA=��AMQ��AN=AD=3��MN=MD=1��
���MAQ=��AMQ��
��MQ=AQ��
��NQ=x����AQ=MQ=1+x��
�ߡ�ANM=90�㣬
���ANQ=90�㣬
��Rt��ANQ�У��ɹ��ɶ����ã�AQ2=AN2+NQ2��
�ࣨx+1��2=32+x2��
��ã�x=4��
��NQ=4��AQ=5��
��AB=4��AQ=5��
��S��NAB=$\frac{4}{5}{S}_{��NAQ}$=$\frac{4}{5}$��$\frac{1}{2}$AN•NQ=$\frac{4}{5}��\frac{1}{2}$��3��4=$\frac{24}{5}$��
��III����ͼ3����A��AH��BF��H��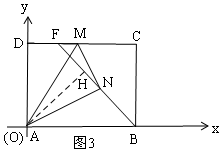
���ı���ABCD�Ǿ��Σ�
��AB��CD��
���AHB=��BCF=90�㣬
���ABH�ס�BFC��
��$\frac{BH}{AH}=\frac{CF}{BC}$��
Rt��AHN����AH��AN=3��AB=4��
�൱��N��H�غϣ���AH=AN��ʱ��AH���BH��С��CF��С��DF���ʱ��M��F�غϣ�B��N��M���㹲�ߣ���ͼ4��ʾ��
���۵��ã�AD=AH��
��AD=BC��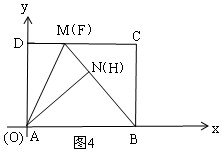
��AH=BC��
�ڡ�ABH�͡�BFC�У�
$\left\{\begin{array}{l}{��HBA=��BFC}\\{��AMB=��BCF}\\{AH=BC}\end{array}\right.$��
���ABH�ա�BFC��AAS����
��CF=BH��
�ɹ��ɶ����ã�BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$��
��CF=$\sqrt{7}$��
��DF�����ֵΪDC-CF=4-$\sqrt{7}$��
���� �������ı��ε��ۺ��⣬������������ȫ�Ⱥ����Ƶ����ʺ��ж����۵������ʡ����ɶ�����ͼ���������ص㡢��������Ǻ���ֵ�����������۵��������ǹؼ���ע��ͼ���������ص㣬��II�ʹ���ֱ�������Σ����ù��ɶ����з����ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
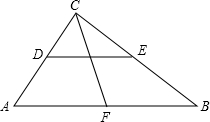
 ��ͼ���ڡ�ABC�У�CE��CF�ֱ�ƽ�֡�ACB�������ڲ��ǡ�ACD��AE��CE��E��AF��CF��F��ֱ��EF�ֱ�AB��AC��M��N��
��ͼ���ڡ�ABC�У�CE��CF�ֱ�ƽ�֡�ACB�������ڲ��ǡ�ACD��AE��CE��E��AF��CF��F��ֱ��EF�ֱ�AB��AC��M��N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
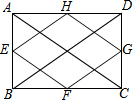 ��ͼ����֪����ABCD�ĶԽ���AC��BD�ij���6cm��E��F��G��H�ֱ���AB��BC��CD��DA���е㣬���ı���EFGH���ܳ��ǣ�������
��ͼ����֪����ABCD�ĶԽ���AC��BD�ij���6cm��E��F��G��H�ֱ���AB��BC��CD��DA���е㣬���ı���EFGH���ܳ��ǣ�������| A�� | 18cm | B�� | 16cm | C�� | 15cm | D�� | 12cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ1���ҹ��Ŵ������ġ���ˬ��ͼ����ʾ��ͼ���������ĸ�ȫ�ȵ�ֱ��������Χ�ɵģ���AC=4��BC=6�����ĸ�ֱ���������б߳�Ϊ4��ֱ�DZ߷ֱ������ӳ�һ�����õ�ͼ2��ʾ�ġ���ѧ�糵����������糵����Χ�ܳ��ǣ�������
��ͼ1���ҹ��Ŵ������ġ���ˬ��ͼ����ʾ��ͼ���������ĸ�ȫ�ȵ�ֱ��������Χ�ɵģ���AC=4��BC=6�����ĸ�ֱ���������б߳�Ϊ4��ֱ�DZ߷ֱ������ӳ�һ�����õ�ͼ2��ʾ�ġ���ѧ�糵����������糵����Χ�ܳ��ǣ�������| A�� | 56 | B�� | 24 | C�� | 64 | D�� | 32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������y=$\frac{4}{x}$��x��0��ͼ����һ��P�ĺ�������4������P��ֱ��l��x���ڵ�A����y�Ḻ�����ڵ�B����OA=OB��
��ͼ������y=$\frac{4}{x}$��x��0��ͼ����һ��P�ĺ�������4������P��ֱ��l��x���ڵ�A����y�Ḻ�����ڵ�B����OA=OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
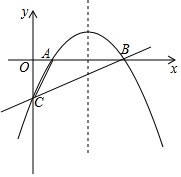 ��ͼ��������y=ax2+bx-2������A��1��0���͵�B��4��0������y�ύ�ڵ�C��
��ͼ��������y=ax2+bx-2������A��1��0���͵�B��4��0������y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC�DZ߳�Ϊ2�ĵȱ������Σ��Խ����ʵ���ֱ������ϵ����������������꣮
��ͼ����֪��ABC�DZ߳�Ϊ2�ĵȱ������Σ��Խ����ʵ���ֱ������ϵ����������������꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90�㣬��F��AB���е㣬CF=8cm������λ��DE=8cm��
��ͼ����Rt��ABC�У���ACB=90�㣬��F��AB���е㣬CF=8cm������λ��DE=8cm���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com