
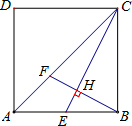
 边长为1的正方形ABCD中,E是AB中点,连CE,过B作BF⊥CE交AC于F,求AF.
边长为1的正方形ABCD中,E是AB中点,连CE,过B作BF⊥CE交AC于F,求AF.| 1 |
| 3 |
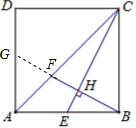 证明:延长BF交AD于G,
证明:延长BF交AD于G,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| ||
| 3 |


科目:初中数学 来源: 题型:
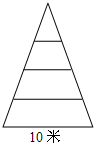 如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为
如图,是一轴截面为等腰三角形的古塔,塔基圆直径为10米,塔共四层,每层高3米,天意广告公司欲沿塔面悬挂一幅公益广告条幅,要求条幅不能铺在地面上,也不能高于塔顶,则条幅的最大长度为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com