
【题目】如图,四边形ABCD内接于⊙O.
(1)连接AC、BD,若∠BAC=∠CAD=60°,则△DBC的形状为 .
(2)在(1)的条件下,试探究线段AD,AB,AC之间的数量关系,并证明你的结论;
(3)若![]() ,∠DAB=∠ABC=90°,点P为
,∠DAB=∠ABC=90°,点P为![]() 上的一动点,连接PA,PB,PD,求证:PD=PB+
上的一动点,连接PA,PB,PD,求证:PD=PB+![]() PA.
PA.
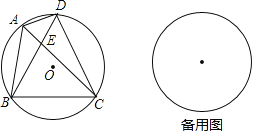
【答案】(1)等边三角形;(2)AC=AB+AD,理由见解析;(3)证明见解析.
【解析】
(1)利用等弧对等角,可以判断出△DBC是等边三角形;
(2)如图1,在AC上截取AE=AD,连接DE,利用等边△DBC以及等边对等角的关系,可以证得△DAB≌△DEC(SAS),可以证明AC=AB+AD;
(3)如图2,根据已知条件易证得四边形ABCD是正方形,在PD上取DE=BP,也同样可证得△DAE≌△BAP(SAS),可证得![]() PAE为等腰直角三角形,所以PE=
PAE为等腰直角三角形,所以PE=![]() PA.
PA.
(1)∵∠BAC=∠BDC=60°,∠CAD=∠CBD=60°,
∴∠BDC=∠CBD=∠BCD=60°,
∴△DBC是等边三角形.
故答案为:等边三角形.
(2)结论:AC=AB+AD.
理由:如图1,在AC上截取AE=AD,连接DE.
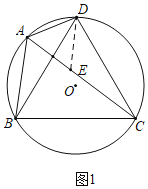
∵∠DAE=60°,AD=AE,
∴△ADE是等边三角形,
∴AD=DE,∠ADE=∠BDC=60°,
∴∠ADB=∠EDC,
∵DA=DE,DB=DC,
∴△DAB≌△DEC(SAS),
∴EC=AB,
∴DE=AD
∴AC=AE+EC=AD+AB.
(3)如图2中,在PD上取DE=BP,
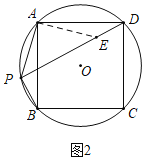
∵∠DAB=∠ABC=90°,
∴∠BCD=∠ADC=90°,
∴四边形ABCD是矩形,
∵![]() ,
,
∴AB=BC,
∴四边形ABCD是正方形,
∴DA=BD,∠ADE=∠ABF,DE=BP,
∴△DAE≌△BAP(SAS),
∴AE=AP,∠DAE=∠BAP,
∴∠PAE=∠BAD=90°,
∴PE=![]() PA,
PA,
∴PD﹣PB=PD=DE=PE=![]() PA.
PA.


科目:初中数学 来源: 题型:
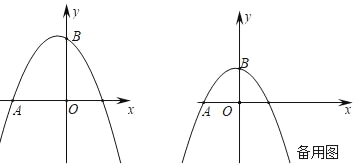
【题目】已知抛物线y=ax2﹣![]() x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
x+c经过A(﹣2,0),B(0,2)两点,动点P,Q同时从原点出发均以1个单位/秒的速度运动,动点P沿x轴正方向运动,动点Q沿y轴正方向运动,连接PQ,设运动时间为t秒
(1)求抛物线的解析式;
(2)当BQ=![]() AP时,求t的值;
AP时,求t的值;
(3)随着点P,Q的运动,抛物线上是否存在点M,使△MPQ为等边三角形?若存在,请求出t的值及相应点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
如:P(1,4)的“2属派生点为P′(1+2×4,2×1+4),即P′(9,6);
(1)点P(-1,3)的“2属派生点”P′的坐标为______;
(2)若点P的“3属派生点”P′的坐标为(-1,3),则点P的坐标为______.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为点P′,线段PP′的长度等于线段OP的长度,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).


查看答案和解析>>
科目:初中数学 来源: 题型:
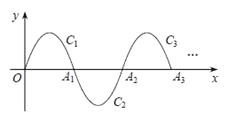
【题目】如图,在平面直角坐标系xOy中,已知抛物线(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x 轴交于另一点A3;将C3绕点A2旋转180°得C4,与x 轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为 ;Cn的顶点坐标为 (n为正整数,用含n的代数式表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,BE,DF,MN是三根直立于地面的木杆在同一灯光下的影子,请画出第三根木杆,(画出示意图,不用写画法)
(2)如图②,小明在阳光下利用标杆AB测量校园内一棵小树CD的高度,在同一时刻测得标杆的影长BE为2 m,小树的影长落在地面上的部分DM为3 m,落在墙上的部分MN为1 m,若标杆AB的长为1.5 m,求小树的高度CD.
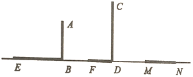
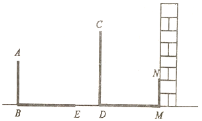
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
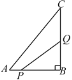
【题目】如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm,若点P从点A沿AB边向B点以1 cm/s的速度移动,点Q从B点沿BC边向点C以2 cm/s的速度移动,两点同时出发.
(1)问几秒后,△PBQ的面积为8cm?
(2)出发几秒后,线段PQ的长为4![]() cm ?
cm ?
(3)△PBQ的面积能否为10 cm2?若能,求出时间;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com