
 如图:A,B是函数
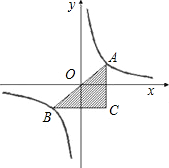
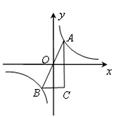
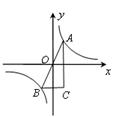
如图:A,B是函数 的图象上关于原点O对称的任意两点.AC平行于y轴,BC平行于x轴,求△ABC的面积.
的图象上关于原点O对称的任意两点.AC平行于y轴,BC平行于x轴,求△ABC的面积.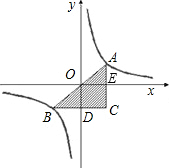 解:如图所示,
解:如图所示, ),则B点坐标为(-x,-
),则B点坐标为(-x,- ),
), ),
), |=1,
|=1, 图象上两点,
图象上两点, k=
k= ,
, +
+ =2.
=2. ),根据A、B两点关于原点对称可知,B点坐标为(-x,-
),根据A、B两点关于原点对称可知,B点坐标为(-x,- ),可求出C点坐标,利用矩形的面积公式可求出矩形OECD的面积,再根据反比例函数中系数k的几何意义可求出△AOE与△BOD的面积,把矩形OECD的面积与两三角形的面积相加即可得出结论.
),可求出C点坐标,利用矩形的面积公式可求出矩形OECD的面积,再根据反比例函数中系数k的几何意义可求出△AOE与△BOD的面积,把矩形OECD的面积与两三角形的面积相加即可得出结论.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源:2013-2014学年山东诸城龙源学校九年级下学期第一次学情检测数学试卷(解析版) 题型:选择题
如图,A,B是函数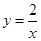 的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则(
).
的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则(
).
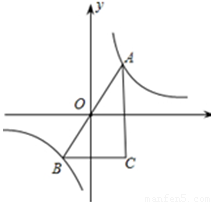
A.S=2 B.S=4 C.2<S<4 D.S>4
查看答案和解析>>
科目:初中数学 来源:2013届浙江丽水莲都区志竞中学八年级下期中数学卷(解析版) 题型:选择题
如图,A、B是函数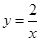 的图象上关于原点对称的任意两点,
的图象上关于原点对称的任意两点,
BC∥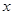 轴,AC∥
轴,AC∥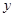 轴,△ABC的面积记为
轴,△ABC的面积记为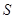 ,则( )
,则( )
A.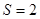 ; B.
; B.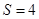 ; C.
; C.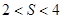 ; D.
; D.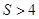 .
.

查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南省周口市初三下学期第二十七章图形的相似检测题 题型:选择题
如图,A、B是函数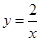 的图象上关于原点对称的任意两点,BC∥
的图象上关于原点对称的任意两点,BC∥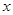 轴,AC∥
轴,AC∥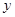 轴,△ABC的面积记为
轴,△ABC的面积记为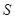 ,则
,则
A. 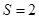 B.
B.
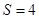 C.
C.  D.
D.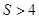
查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市顺义区九年级数学第一次统练试卷 题型:选择题
如图,A、B是函数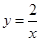 的图象上关于原点对称的任意两点,BC∥
的图象上关于原点对称的任意两点,BC∥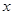 轴,AC∥
轴,AC∥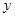
轴,△ABC的面积记为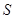 ,则
,则
A. 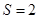 B.
B.
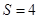
C. 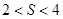 D.
D.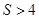
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com