
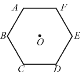
【题目】如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O旋转多少度后能和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
【答案】(1) 直线AD、BE、CF以及线段AB、BC、CD的垂直平分线;(2) 60°或60°的整数倍; (3) ![]() 或其整数倍.
或其整数倍.
【解析】
(1)根据对称轴的意义:正六边形ABCDEF的对称轴为过中心O与顶点的对角线,过中心O与边垂直的直线.
(2)正六边形ABCDEF是中心对称与轴对称的图形,故这个正六边形绕点O旋转60°或其整数倍后能和原来的图形重合.
(3)根据轴对称的意义,可得答案.
(1)直线AD、BE、CF以及线段AB、BC、CD的垂直平分线都是这个正六边形的对称轴.
(2)因为正六边的中心角为60°,正六边形绕点O旋转60°或其整数倍后能和原来的图形重合.
(3)一般地,正n边形每条边的垂直平分线都是对称轴;
当n是偶数时,相对顶点的连线也是对称轴;
绕正n边形的中心旋转![]() 或其整数倍都能与原来的图形重合.
或其整数倍都能与原来的图形重合.


科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)某顾客在此商场购物220元,通过转转盘获得购物券和直接获得购物券,你认为哪种方式对顾客更合算?谈谈你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
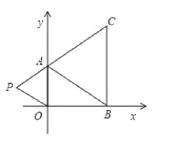
【题目】如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a.b.c满足关系式![]() ,c是64的算术平方根.
,c是64的算术平方根.
(1)直接写出a,b,c的值:a=____,b=____,c= ____;
(2)如果在第二象限内有一点P(m,2),请用含m的式子表示四边形APOB的面积S![]() ;
;
(3)在(2)的条件下,是否存在点P,使四边形APOB的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
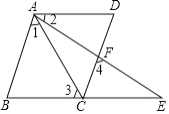
【题目】填空:已知:如图,![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() ,
,![]() .求证:
.求证:![]() .
.
证明:∵![]()
∴________(内错角相等,两直线平行)
∴![]() ________(两直线平行,内错角相等)
________(两直线平行,内错角相等)
∵![]()
∴![]() (________________)
(________________)
∵![]()
∴![]() ,(________________)
,(________________)
即![]() ________
________
∴![]()
∴![]() (同位角相等,两直线平行).
(同位角相等,两直线平行).
查看答案和解析>>
科目:初中数学 来源: 题型:
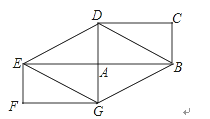
【题目】如图,矩形ABCD和矩形AEFG关于点A中心对称,
(1)四边形BDEG是菱形吗?请说明理由.
(2)若矩形ABCD面积为8,求四边形BDEG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为 . 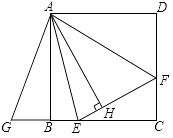
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com