
已知点P是直线 (
(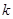 >0,)上一定点,点A是
>0,)上一定点,点A是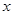 轴上一动点(不与原点重合),连结PA,过点P作PB⊥PA,交
轴上一动点(不与原点重合),连结PA,过点P作PB⊥PA,交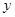 轴于点B,探究线段PA与PB 的数量关系.
轴于点B,探究线段PA与PB 的数量关系.
【小题1】如图(1),当PA⊥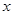 轴时,观察图形发现线段PA与PB的数量关系是__________;
轴时,观察图形发现线段PA与PB的数量关系是__________;
【小题2】当PA与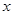 轴不垂直时,在图(2)中画出图形,线段PA与PB 的数量关系是否与(Ⅰ)所得结果相同?写出你的猜想并加以证明;
轴不垂直时,在图(2)中画出图形,线段PA与PB 的数量关系是否与(Ⅰ)所得结果相同?写出你的猜想并加以证明;
【小题3】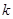 为何值时,线段PA=PB?此时∠POA的度数是多少,为什么?
为何值时,线段PA=PB?此时∠POA的度数是多少,为什么?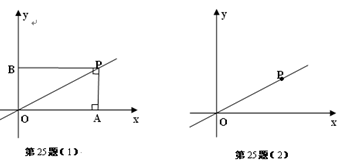
【小题1】PA=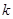 PB. ……2分
PB. ……2分
【小题2】如图2,过P 作PC⊥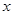 轴于C,PD⊥
轴于C,PD⊥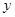 轴于D,设P(
轴于D,设P( ,
,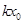 ).
).
∵∠BPD+∠DPA=∠APB=90°,∠APC+∠DPA=∠CPD=90°,
∴∠APC=∠BPD.∴Rt△APC∽Rt△BPD. ……4分
∴ .∴
.∴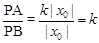 .∴PA=
.∴PA=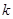 PB. ……6分
PB. ……6分
【小题3】当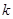 =1时,PA=PB,此时∠POA=45°或∠POA=135°.……8分
=1时,PA=PB,此时∠POA=45°或∠POA=135°.……8分
这是因为 由(Ⅱ)得PA=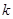 PB,所以当
PB,所以当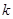 =1时,PA=PB.
=1时,PA=PB.
此时Rt△APC≌Rt△BPD,∴PC=PD,
即点P到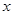 轴、
轴、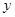 轴的距离相等,所以直线
轴的距离相等,所以直线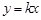 (
(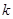 =1)平分一、三象限的夹角.
=1)平分一、三象限的夹角.
∴∠POA=45°或∠POA=135°(如图3). ……10分
解析


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC的角平分线.
如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC的角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.| 2n |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com