
 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 设D点坐标为(x,1),0<x<1,E(1,y),根据勾股定理列出关于x的等式即可求解.
解答 解:设D点坐标为(x,1),
∵动点D在线段BC上移动(不与B,C重合),
∴0<x<1,
∵DE⊥OD,
∴OD2+DE2=OE2,
∴x2+1+(x-1)2+(y-1)2=1+y2,
解得:y=x2-x+1,
∴1+y2=1+(x2-x+1)2=1+[(x-$\frac{1}{2}$)2+$\frac{3}{4}$]2,
当x=$\frac{1}{2}$时,线段OE取得最小值,
最小值为:OE=$\sqrt{1+\frac{9}{16}}$=$\frac{5}{4}$=1.25,
∴AE=$\sqrt{O{E}^{2}-O{A}^{2}}$=$\frac{3}{4}$,
故选C.
点评 本题主要考查了正方形的性质,二次函数的最值,勾股定理,难度不大,关键是掌握用配方法求二次函数最值.


科目:初中数学 来源: 题型:解答题
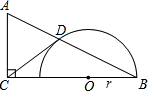 如图,在Rt△ABC中,已知∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边交于点D,连结CD,恰好AC=DC.
如图,在Rt△ABC中,已知∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边交于点D,连结CD,恰好AC=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
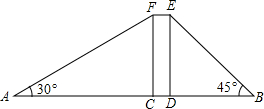 宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,不有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们量一量把!”君哥、宾哥在楼体两侧各选A、B两点,其中CDEF表示楼体,AB=200米,CD=20米.∠A=30°,∠B=45°,(A、C、D、E四点在同一直线上)问:
宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,不有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们量一量把!”君哥、宾哥在楼体两侧各选A、B两点,其中CDEF表示楼体,AB=200米,CD=20米.∠A=30°,∠B=45°,(A、C、D、E四点在同一直线上)问:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
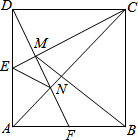 如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )
如图,正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于N,交AB于F,连接EN、BM,有如下结论:①△ADF≌△DCE;②MN=FN;③BM=BC;④S△ADN:S四边形CNFB=2:5;⑤∠ADF=∠BMF.其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 近年来,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.
近年来,中国中东部大部分地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了尚不完整的统计图表.| 组 | 观点 | 人数 |
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 | M |
| C | 汽车尾部排放 | N |
| D | 工厂造成污染 | 120 |
| E | 其他 | 60 |
| A. | 200 | B. | 240 | C. | 440 | D. | 480 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某商品的商标,由七个形状、大小完全相同的正六边形组成.我们称正六边形的顶点为格点,已知△ABC的顶点都在格点上,且AB边位置如图所示,则△ABC是直角三角形的个数有( )
如图是某商品的商标,由七个形状、大小完全相同的正六边形组成.我们称正六边形的顶点为格点,已知△ABC的顶点都在格点上,且AB边位置如图所示,则△ABC是直角三角形的个数有( )| A. | 6个 | B. | 8个 | C. | 10个 | D. | 12个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).
平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com