
【题目】如图,抛物线![]() 与坐标轴分别交于
与坐标轴分别交于![]() ,
,![]() ,
,![]() 三点,连接
三点,连接![]() ,
,![]() .
.
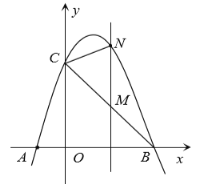
(1)直接写出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(2)点![]() 是线段
是线段![]() 上一点(不与
上一点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,连接
,连接![]() .若点
.若点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在
恰好在![]() 轴上,求出点
轴上,求出点![]() 的坐标;
的坐标;
(3)在平面内是否存在一点![]() ,使
,使![]() 关于点
关于点![]() 的对称
的对称![]() (点
(点![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() 的对称点)恰好有两个顶点落在该抛物线上?若存在,求出点
的对称点)恰好有两个顶点落在该抛物线上?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在点
;(3)存在点![]() 或
或![]() ,使
,使![]() 关于点
关于点![]() 的对称
的对称![]() 恰好有两个顶点落在该抛物线上.
恰好有两个顶点落在该抛物线上.
【解析】
(1)分别令y=0,x=0,代入![]() ,即可得到答案;
,即可得到答案;
(2)由点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,且点
对称,且点![]() 在y轴上,
在y轴上,![]() 轴,得
轴,得![]() ,易得直线
,易得直线![]() 的解析式为:
的解析式为:![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,则
,则![]() ,
,![]() ,列出关于t的方程,即可求解;
,列出关于t的方程,即可求解;
(3)根据题意,![]() 平行于
平行于![]() 轴,
轴,![]() 平行于
平行于![]() 轴,
轴,![]() ,
,![]() ,点
,点![]() 在点
在点![]() 的右边,点
的右边,点![]() 在点
在点![]() 的下方,设点
的下方,设点![]() 的横坐标为
的横坐标为![]() ,则
,则![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,分三种情况讨论:①若
,分三种情况讨论:①若![]() 、
、![]() 在抛物线上,②若
在抛物线上,②若![]() 、
、![]() 在抛物线上,③
在抛物线上,③![]() ,
,![]() 不可能同时在抛物线上,即可得到答案.
不可能同时在抛物线上,即可得到答案.
(1)令y=0,代入![]() ,得
,得![]() ,解得:
,解得:![]() ,
,
令x=0,代入 ![]() ,得: y=3,
,得: y=3,
∴![]() ,
,![]() ,
,![]() ;
;
(2)∵点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,且点
对称,且点![]() 在y轴上,
在y轴上,
∴![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
把![]() ,
,![]() ,代入
,代入![]() ,得:
,得:![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
设点![]() 的横坐标为
的横坐标为![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),
(舍去),
∴![]() ;
;
(3)根据题意,![]() 平行于
平行于![]() 轴,
轴,![]() 平行于
平行于![]() 轴,
轴,![]() ,
,![]() ,点
,点![]() 在点
在点![]() 的右边,点
的右边,点![]() 在点
在点![]() 的下方,设点
的下方,设点![]() 的横坐标为
的横坐标为![]() ,则
,则![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
①若![]() 、
、![]() 在抛物线上,则
在抛物线上,则![]()
∴![]()
∴![]()
∵点O与O′关于点P中心对称,即点P 是OO′的中点,
∴![]() ;
;
②若![]() 、
、![]() 在抛物线上,则
在抛物线上,则![]() ,
,
解得:![]() ,
,
∴![]()
同①可得:![]() ;
;
③![]() ,
,![]() 不可能同时在抛物线上,
不可能同时在抛物线上,
综上所述存在点![]() 或
或![]() ,使
,使![]() 关于点
关于点![]() 的对称
的对称![]() 恰好有两个顶点落在该抛物线上.
恰好有两个顶点落在该抛物线上.



科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+6与y轴交于点A,与x轴交于点B,点E为线段AB的中点,∠ABO的平分线BD与y轴相交于点D,A、C两点关于x轴对称.
x+6与y轴交于点A,与x轴交于点B,点E为线段AB的中点,∠ABO的平分线BD与y轴相交于点D,A、C两点关于x轴对称.

(1)一动点P从点E出发,沿适当的路径运动到直线BC上的点F,再沿适当的路径运动到点D处.当P的运动路径最短时,求此时点F的坐标及点P所走最短路径的长;
(2)点E沿直线y=3水平向右运动得点E',平面内是否存在点M使得以D、B、M、E'为顶点的四边形为菱形,若存在,请直接写出点E′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,点O在AB上,以点O为圆心,OA为半径的圆与BC相切与点D,与AC相交与点E,若CD=6,则CE=__.
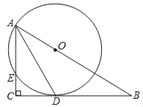
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另-个转出蓝色即可配成紫色,则可配成紫色的概率是( )
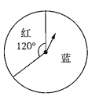
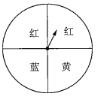
转盘一 转盘二
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(问题发现)
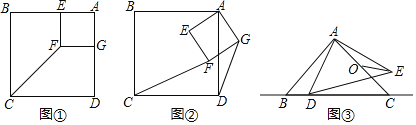
如图①,正方形AEFG的两边分别在正方形ABCD的边AB和AD上,连接CF.
填空:①线段CF与DG的数量关系为 ;
②直线CF与DG所夹锐角的度数为 .
(2)(拓展探究)
如图②,将正方形AEFG绕点A逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.
(3(解决问题)
如图③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC的中点.若点D在直线BC上运动,连接OE,则在点D的运动过程中,线段OE长的最小值为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(Ⅰ)已知![]() ,若二次函数图象与
,若二次函数图象与![]() 轴有唯一公共点,求
轴有唯一公共点,求![]() 的值;
的值;
(Ⅱ)已知![]() .
.
(ⅰ)当![]() 时,二次函数图象与
时,二次函数图象与![]() 轴有且只有一个公共点,求
轴有且只有一个公共点,求![]() 的取值范围;
的取值范围;
(ⅱ)当![]() 时,
时,![]() 有最小值
有最小值![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
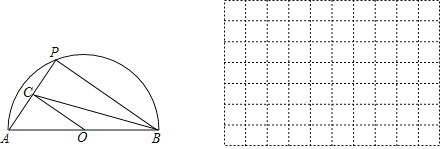
【题目】如图,P是半圆弧![]() 上一动点,连接PA、PB,过圆心O作
上一动点,连接PA、PB,过圆心O作![]() 交PA于点C,连接
交PA于点C,连接![]() 已知
已知![]() ,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
,设O,C两点间的距离为xcm,B,C两点间的距离为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是小东的探究过程,请补充完整:
![]() 通过取点、画图、测量,得到了x与y的几组值,如下表:
通过取点、画图、测量,得到了x与y的几组值,如下表:
| 0 |
| 1 |
| 2 |
| 3 |
| 3 |
|
|
|
| 6 |
![]() 说明:补全表格时相关数据保留一位小数
说明:补全表格时相关数据保留一位小数![]()
![]() 建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
![]() 结合画出的函数图象,解决问题:直接写出
结合画出的函数图象,解决问题:直接写出![]() 周长C的取值范围是______.
周长C的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿射线BC平移得到△A′B′C′,使得点A′落在∠ABC的平分线BD上,连接AA′,AC′.
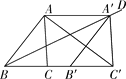
(1)判断四边形ABB′A′的形状,并证明;
(2)在△ABC中,AB=6,BC=4,若AC′⊥A′B′,求四边形ABB′A′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
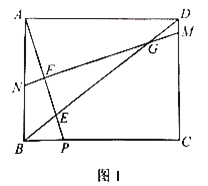
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
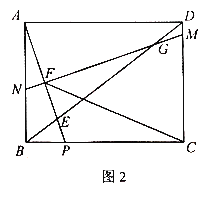
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com