
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 根据平移性质得出B点向左平移2个单位,再向下平移2个单位得到B′,根据规律求出A′、C的坐标,过B作BD⊥AC于D,根据点的坐标求出AC,BD的长,根据三角形面积公式求出即可.
解答 解:∵把△ABC经过平移后得到△A′B′C′,B(3,1)的对应点是B′(1,-1),
∴B点向左平移2个单位,再向下平移2个单位,
∵A(4,3)的对应点A′的坐标是(4-2,3-2),即A′(2,1),
C′(2,0))的对应点C的坐标是(2+2,0+2),即(4,2),
过B作BD⊥AC于D,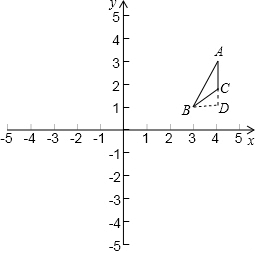
∵A(4,3),C(4,2),
∴AC⊥X轴,
∴AC=3-2=1,BD=4-3=1,
∴△ABC的面积是$\frac{1}{2}$AC×BD=$\frac{1}{2}$×1×1=$\frac{1}{2}$.
答:△ABC的面积是$\frac{1}{2}$.
点评 本题主要考查对坐标与图形变化-平移,平移的性质,三角形的面积等知识点的理解和掌握,能根据平移性质进行计算是解此题的关键.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
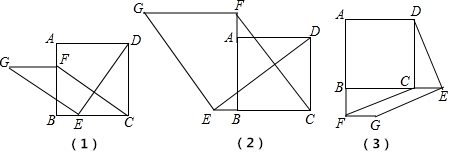
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解全市中学生的课外阅读情况,选择全面调查 | |
| B. | 旅客上飞机前的安检,选择全面调查 | |
| C. | 为了了解《人民的名义》的收视率,选择抽样调查 | |
| D. | 为保证“神舟十一号”载人飞船的成功发射,对其零部件的检查,选择全面调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
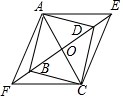 如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF.
如图,在?ABCD中,对角线AC、BD相交于点O,OA=5cm,E、F为直线BD上的两个动点(点E、F始终在?ABCD的外面),且DE=$\frac{1}{2}$OD,BF=$\frac{1}{2}$OB,连接AE、CE、CF、AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com