
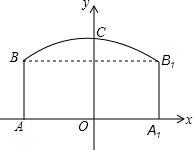
 如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系.
如图,隧道的截面由抛物线和长方形构成.长方形的长为12m,宽为5m,抛物线的最高点C离路面AA1的距离为8m,建立如图所示的直角坐标系.分析 (1)根据函数图象经过顶点(0,8)和点(6,5)可以求得该函数的解析式以及确定自变量x的取值范围;
(2)根据题意将x=4代入(1)中求得函数值,然后与6比较,即可解答本题.
解答 解:(1)设抛物线的解析式为y=ax2+8,
∵函数经过点(6,5),
∴5=a×62+8,得a=$-\frac{1}{12}$,
即该抛物线的解析式为y=$-\frac{1}{12}{x}^{2}+8$(-6≤x≤6);
(2)∵该隧道内设双向行车道,
∴该货车只能走一个车道,
∴将x=4代入y=$-\frac{1}{12}{x}^{2}+8$,得y=$6\frac{2}{3}$,
∵$6\frac{2}{3}$>6,
∴这辆货车能安全通过.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)的图象过(2,3).
在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)的图象过(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
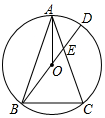 如图,△ABC中,AB=AC,⊙O为△ABC外接圆,BD为⊙O直径,DB交AC于E.连接AO
如图,△ABC中,AB=AC,⊙O为△ABC外接圆,BD为⊙O直径,DB交AC于E.连接AO查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com