
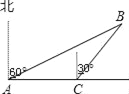
【题目】某民航飞机在大连海域失事,为调查失事原因,决定派海军潜水员打捞飞机上的黑匣子,如图所示,一潜水员在A处以每小时8海里的速度向正东方向划行,在A处测得黑匣子B在北偏东60°的方向,划行半小时后到达C处,测得黑匣子B在北偏东30°的方向,在潜水员继续向东划行多少小时,距离黑匣子B最近,并求最近距离.
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A. 两个相似三角形面积比为2:3,则周长比是4:9
B. 相似图形一定构成位似图形
C. 如果点D、E分别在△ABC的边AB、AC上,△ABC与△ADE相似,则DE∥BC
D. 在Rt△ABC中,斜边上的高CD2=ADBD
查看答案和解析>>
科目:初中数学 来源: 题型:
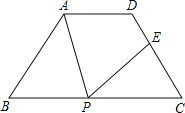
【题目】如图,四边形ABCD中,AD∥BC,AB=DC,AD=3cm,BC=7cm,∠B=60°,P为BC边上一点(不与B,C重合),连接AP,过P点作PE交DC于E,使得∠APE=∠B.
(1)求证:△ABP∽△PCE;
(2)求AB的长;
(3)在边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各变量之间是反比例关系的是( )
A. 存入银行的利息和本金 B. 在耕地面积一定的情况下,人均占有耕地面积与人口数
C. 汽车行驶的时间与速度 D. 电线的长度与其质量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是![]() 上一点(不与C、D重合),求证:∠CPD=∠COB;
上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
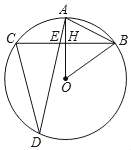
【题目】如图,⊙O的半径OA⊥弦BC于H,D是⊙O上另一点,AD与BC相交于点E,若DC=DE,OB=![]() ,AB=5.
,AB=5.
(1)求证:∠AOB=2∠ADC.
(2)求AE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
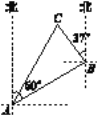
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(﹣1311,y1),(﹣1312,y2),(1314,y3)在反比例函数y=﹣![]() 图象上,则下列结论正确的是( )
图象上,则下列结论正确的是( )
A. y3>y1>y2 B. y2>y1>y3 C. y1>y2>y3 D. y3>y2>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点, ![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
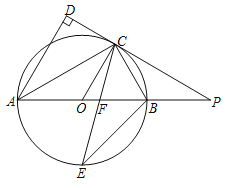
(1)求证: ![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com