
如图,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC,求:
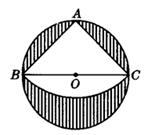
(1)被剪掉的阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆半径是多少?(结果可用根号表示)
(1)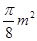 ;(2)
;(2)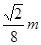
【解析】
试题分析:(1)先根据圆周角定理可得弦BC为直径,即可得到AB=AC,根据特殊角的锐角三角函数值可求得AB的长,最后根据扇形的面积公式即可求得结果;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,根据弧长公式及圆的周长公式即可求得结果.
(1)∵∠BAC=90°
∴弦BC为直径
∴AB=AC
∴AB=AC=BC·sin45°=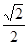
∴S阴影=S⊙O-S扇形ABC=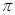 (
(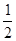 )2-
)2-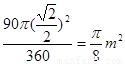 ;
;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,由题意得
2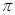 r=
r=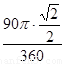 ,解得r=
,解得r=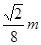
答:(1)被剪掉的阴影部分的面积为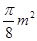 ;(2)该圆锥的底面圆半径是
;(2)该圆锥的底面圆半径是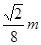 .
.
考点:圆周角定理,特殊角的锐角三角函数值,扇形的面积公式,弧长公式
点评:计算能力是初中数学学习中一个极为重要的能力,是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.


科目:初中数学 来源: 题型:
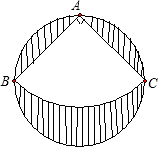 如图,有一直径为1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC
如图,有一直径为1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC.
如图所示,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC.查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:059
如图所示,有一直径为1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形BAC.求:
(1)被剪掉阴影部分的面积;
(2)用剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆半径是多少?(结果可保留根号)
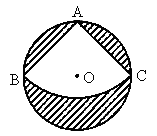
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,有一直径是1m的圆形铁皮,要从中剪出一个圆心角为90°的扇形ABC。
(1)求被剪掉的阴影部分的面积;
(2)用所剪的扇形铁皮围成一个圆锥,该圆锥的底面半径是多少?(结果可用根号表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com