
【题目】如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.
(1)已知旗杆高为12米,若在点B处测得旗杆顶点E的仰角为30°,A处测得点E的仰角为45°,试求AB的长(结果保留根号);
(2)在(1)的条件下,若∠BCA=45°,绳子在空中视为一条线段,试求绳子AC的长(结果保留根号)?
【答案】
(1)
解:∵在直角△BEF中,tan∠EBF= ![]() ,
,
∴BE= ![]() =
= ![]() =12
=12 ![]() .
.
同理AF=EF=12(米),
则AB=BF+AF=12 ![]() +12(米)
+12(米)
(2)
解:作AG⊥BE于点G,
在直角△ABG中,AG=ABsin30°= ![]() (12
(12 ![]() +12)=6
+12)=6 ![]() +6.
+6.
又∵直角△AGC中,∠ACG=45°,
∴AC= ![]() AG=6
AG=6 ![]() +6
+6 ![]() (米).
(米).

【解析】(1)在直角△BEF中首先求得BF,然后在直角△AEF中求得AF,根据AB=BF+AF即可求解;(2)作AG⊥BC于点G,在直角△ABG中首先求得AG,然后在直角△AGC中利用三角函数求解.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于1<
的小数部分我们不可能全部地写出来,但是由于1<![]() <2,所以
<2,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,差就是小数部分
减去其整数部分1,差就是小数部分![]() -1,根据以上的内容,解答下面的问题:
-1,根据以上的内容,解答下面的问题:
(1)![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(2)1+![]() 的整数部分是 ,小数部分是 ;
的整数部分是 ,小数部分是 ;
(3)若设2+![]() 整数部分是x,小数部分是y,求x-y的值.
整数部分是x,小数部分是y,求x-y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于点O,A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( ) 
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100m、200m、1000m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用T1、T2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率P为;
(2)该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率P1 , 利用列表法或树状图加以说明;
(3)该同学从5个项目中任选两个,则两个项目都是径赛项目的概率P2为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即![]()
![]() ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
【动手一试】
试将![]() 改成两个整数平方之和的形式.
改成两个整数平方之和的形式. ![]() ;
;
【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式![]() 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式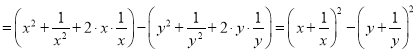 ﹒
﹒
【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式![]() 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )
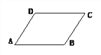
A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
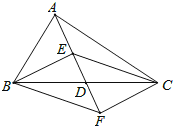
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
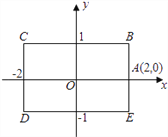
A. (2,0) B. (﹣1,1) C. (﹣2,1) D. (﹣1,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com