
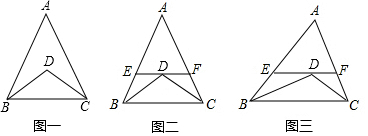
分析 (1)①由条件可证得∠DBC=∠DCB,所以共有两个等腰三角形;
②由平行和角平分线的性质可得∠EDB=∠EBD,∠FDC=∠FCD,且AE=AF,所以增加了三个等腰三角形;
(2)此时同②只能得出∠EDB=∠EBD,∠FDC=∠FCD,即只有两个等腰三角形,且EF=BE+FC.
解答 解:(1)①∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CD分别是角平分线,
∴∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ACB=∠DCB,
∴DB=DC,
∴△BDC是等腰三角形,
即在图1中共有两个等腰三角形;
②∵EF∥BC,
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠DBE=∠DBC,
∴∠DBE=∠EDB,
∴EB=ED,
∴△EBD为等腰三角形,同理△FDC为等腰三角形,
∵EF∥BC,
∴∠AEF=∠AFE,
∵AB=AC,
∴△AEF为等腰三角形,
即在图2中增加了三个等腰三角形;
(2)同②可证明得△EBD为等腰三角形,△FDC为等腰三角形,
所以EF=BE+CF,
即只有两个等腰三角形.
点评 本题主要考查等腰三角形的判定,掌握等腰三角形的判定方法是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
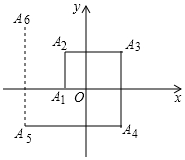 如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为(-2008,-2006),.
如图,一个机器人从点O出发,向正西方向走2m到达点A1;再向正北方向走4m到达点A2;再向正东方向走6m到达点A3;再向正南方向走8m到达点A4;再向正西方向走10m到达点A5;…,按如此规律走下去,当机器人走到点A2017时,点A2017的坐标为(-2008,-2006),.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
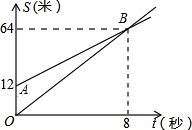 如图,OB,AB分别表示甲乙两名同学运动的一次函数图象,图中s与t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:
如图,OB,AB分别表示甲乙两名同学运动的一次函数图象,图中s与t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 14 | 15 | 23 | 16 | 20 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
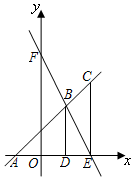 如图,在直角坐标系中,点C在直线AB上,点A、B的坐标分别是(-1,0),(1,2),点C的横坐标为2,过点B作BD⊥x轴于D,过点C作CE⊥x轴于E,直线BE与y轴交于点F.
如图,在直角坐标系中,点C在直线AB上,点A、B的坐标分别是(-1,0),(1,2),点C的横坐标为2,过点B作BD⊥x轴于D,过点C作CE⊥x轴于E,直线BE与y轴交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com