
【题目】超市将某品牌的洗涤液按照进价提高50%后标价,再打八折销售,仍可获利30元.则这种商品的进价是_____元.
 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣2|﹣(2﹣π)0+![]() +(﹣2)3
+(﹣2)3
(2)(﹣2x3)2(﹣x2)÷[(﹣x)2]3
(3)(x+y)2(x﹣y)2
(4)(x﹣2y+3z)(x+2y﹣3z)
查看答案和解析>>
科目:初中数学 来源: 题型:
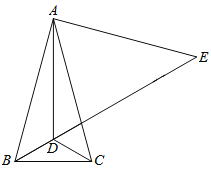
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)=;
(2)(x﹣1)(x2+x+1)=;
(3)(x﹣1)(x3+x2+x+1)=;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)=;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点B(﹣2,2),过反比例函数y=![]() (x<0,常数k<0)图象上一点A(﹣
(x<0,常数k<0)图象上一点A(﹣![]() ,m)作y轴的平行线交直线l:y=x+2于点C,且AC=AB.
,m)作y轴的平行线交直线l:y=x+2于点C,且AC=AB.
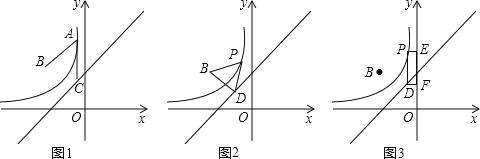
(1)分别求出m、k的值,并写出这个反比例函数解析式;
(2)发现:过函数y=![]() (x<0)图象上任意一点P,作y轴的平行线交直线l于点D,请直接写出你发现的PB,PD的数量关系 ;
(x<0)图象上任意一点P,作y轴的平行线交直线l于点D,请直接写出你发现的PB,PD的数量关系 ;
应用:①如图2,连接BD,当△PBD是等边三角形时,求此时点P的坐标;
②如图3,分别过点P、D作y的垂线交y轴于点E、F,问是否存在点P,使得矩形PEFD的周长取得最小值?若存在,请求出此时点P的坐标及矩形PEFD的周长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学5次数学小测验的成绩分别为(单位:分):90,85,90,95,100,则该同学这5次成绩的众数是( )
A.90 分B.85 分C.95 分D.100 分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com