
 甲、乙两人同时登山,甲、下两人距地面的高度y(单位:米)与登山时间x(单位:分)之间的函数图象如图所示,根据图象提供的信息解答下列问题:
甲、乙两人同时登山,甲、下两人距地面的高度y(单位:米)与登山时间x(单位:分)之间的函数图象如图所示,根据图象提供的信息解答下列问题:分析 (1)根据函数图象由甲走的路程÷时间就可以求出甲的速度;根据函数图象可以求出乙在提速前每分离开地面的高度是15米,就可以求出b的值;
(2)乙提速后,乙的速度是甲登山速度的3倍,所以乙的速度是30米/分.那么求出点B的坐标,加上点A的坐标代入一次函数解析式即可求出乙的函数解析式,把C、D坐标代入一次函数解析式可求出甲的函数解析式;
(3)由(2)的解析式建立方程求出其解就可以求出追上的时间,就可以求出乙离地面的高度,再减去A地的高度就可以得出结论.
解答 解:(1)由函数的图象,得
甲的速度是:(300-100)÷20=10米/分;
b的值为:15×2=30米.
故答案为:10,30;
(2)设y甲=k1x+b1,由函数图象,得
$\left\{\begin{array}{l}{100{=b}_{1}}\\{300=20{k}_{1}+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=10}\\{{b}_{1}=100}\end{array}\right.$,
∴y甲=10x+100;
当0≤x≤2时,y乙=15x;
当2<x≤11时,设直线AB的解析式为:y=k2x+b2
∵乙提速后,乙的速度是甲登山速度的3倍,
∴乙提速后的速度为:30米/分,
∴乙从A到B的时间为:(300-30)÷30=9,
∴t=2+9=11,
∴B(11,300),
∴$\left\{\begin{array}{l}{30=2{k}_{2}+{b}_{2}}\\{300=11{k}_{2}+{b}_{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=30}\\{{b}_{2}=-30}\end{array}\right.$,
∴y乙=30x-30,
∴乙提速后的y与x的关系式为:y乙=30x-30;
∴折线OAB的解析式为:y乙=$\left\{\begin{array}{l}{15x(0≤x≤2)}\\{30x-30(2<x≤11)}\end{array}\right.$;
(3)当y甲=y乙时,
∴10x+100=30x-30,
∴x=6.5,
当x=6.5时,
y乙=30×6.5-30=165
∴乙追上了甲此时乙距A地的高度为:165-30=135米.
点评 本题考查了行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的运用,解答时求出一次函数的解析式是关键


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
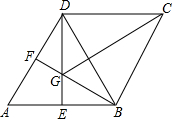 如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交天点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG ③△BDF≌△CGB ④S四边形AEGF=S△BDG,其中正确结论的个数是( )
如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点DE、BF相交天点G,连接BD、CG.有下列结论:①∠FGE=120° ②BG+DG=CG ③△BDF≌△CGB ④S四边形AEGF=S△BDG,其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
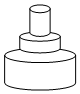 如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )
如图,匀速地向该容器内注水,最后把容器注满,在注水过程中容器内液面的高度h随时间t变化的函数图象最接近实际情况的是( )| A. | 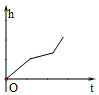 | B. | 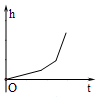 | C. | 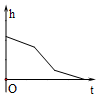 | D. | 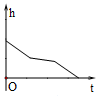 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某班学生的身高情况 | |
| B. | 调查某批次灯泡的使用寿命 | |
| C. | 调查某舞蹈队成员的鞋码大小 | |
| D. | 调查班级某学习小组成员周末写作业的时间 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com