

分析 (1)如图1中.延长BP交AC于H,利用平行线的性质以及三角形的外角的性质即可解决问题.
(2)若点P在射线DF上时,结论:∠1=∠2+∠3.若点P在射线CE上时,结论:∠PBD=∠BPA+∠PAC,证明方法类似.
解答 解:(1)结论:∠2=∠3+∠1.
理由:如图1中.延长BP交AC于H,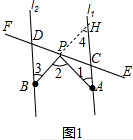
∵BD∥AH,
∴∠3=∠4,
∵∠2=∠1+∠4,
∴∠2=∠1+∠3,
故答案为∠2=∠1+∠3.
(2)若点P在射线DF上时,结论:∠1=∠2+∠3.
理由:如图2中,设AF与BD交于点H.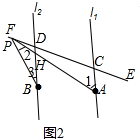
∵BD∥AC,
∴∠AHB=∠1,
∵∠AHB=∠2+∠3,
∴∠1=∠2+∠3.
若点P在射线CE上时,结论:∠PBD=∠BPA+∠PAC,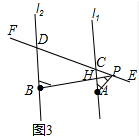
理由:如图3中,设BE与CA交于点H.
∵BD∥AC,
∴∠PBD=∠PHC,
∵∠PHC=∠PAC+∠BPA,
∴∠PBD=∠BPA+∠PAC,
点评 本题考查平行线的性质,解题的关键是记住平行线的性质,学会条件常用辅助线,属于中考常考题型.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为估算学校的旗杆的高度,身高1.8米的小明同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )
如图,为估算学校的旗杆的高度,身高1.8米的小明同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m,BC=8m,则旗杆的高度是( )| A. | 6.4m | B. | 7m | C. | 8m | D. | 9 m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.已知AB∥CD,试猜测∠BED、∠B和∠D满足的数量关系,并试说明理由.
如图.已知AB∥CD,试猜测∠BED、∠B和∠D满足的数量关系,并试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD内部有一点P,AP=1,BP═2,DP=$\sqrt{2}$,将△APD沿AP所在直线翻折得到△APD1,且AD1与BP、BD分别交于E、O两点,PD1与BD交于点F,下列结论:①∠BPD=135°;②BC=$\sqrt{5}$;③连接EF,则EF=$\frac{1}{2}$;④S△DBP=$\frac{2}{3}$S△ABP;其中正确的结论有①②③(填番号)
如图,在正方形ABCD内部有一点P,AP=1,BP═2,DP=$\sqrt{2}$,将△APD沿AP所在直线翻折得到△APD1,且AD1与BP、BD分别交于E、O两点,PD1与BD交于点F,下列结论:①∠BPD=135°;②BC=$\sqrt{5}$;③连接EF,则EF=$\frac{1}{2}$;④S△DBP=$\frac{2}{3}$S△ABP;其中正确的结论有①②③(填番号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com