
分析 (1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据用3000元购进甲种图书的数量=用2400元购进乙种图书的数量列出方程求解即可;
(2)由于购买甲种图书x本,则购买乙种图书(100-x)本,根据:总利润=甲种图书的总利润+乙种图书的总利润可列函数关系式;
(3)根据用不超过1800元购进两种图书,且甲种图书至少购进40本列出不等式组,解不等式组求出解集,从而确定方案,进而求出利润最大的方案.
解答 解:(1)设甲图书的单价为x元/本,则乙图书的单价为(x-4)元/本,根据题意,
得:$\frac{3000}{x}$=$\frac{2400}{x-4}$,
解得:x=20,
经检验x=20是原方程的根,
则x-4=16,
答:甲图书的单价为20元/本,乙图书的单价为16元/本;
(2)根据题意,有:
y=(30-20)x+(25-16)(100-x)=x+900;
(3)根据题意,得:$\left\{\begin{array}{l}{20x+16(100-x)≤1800}\\{x≥40}\end{array}\right.$,
解得:40≤x≤50,
∵x需取整数,
∴x的值可以是:40,41,42,43,44,45,46,47,48,49,50,
故购买方案有11种.
∵y=x+900,k=1>0,
∴y随x的增大而增大,
∴x取最大值50时,y有最大值,
故购买方案有11种.利润最大的方案是:购买甲种图书50本,购买乙种图书50本.
点评 本题考查了一次函数的应用,分式方程的应用,一元一次不等式组的应用,理解题意找到题目蕴含的相等关系或不等关系是解应用题的关键.


科目:初中数学 来源: 题型:解答题
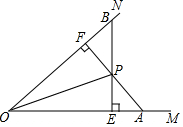 如图,已知点P是∠MON平分线上的一点,PE⊥OM,垂足为E,PF⊥ON,垂足为F,延长FP,交OM于点A,延长EP,交ON于点B,求证:PA=PB.
如图,已知点P是∠MON平分线上的一点,PE⊥OM,垂足为E,PF⊥ON,垂足为F,延长FP,交OM于点A,延长EP,交ON于点B,求证:PA=PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
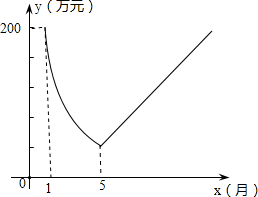 我省某化工厂2013年1月的利润为200万元,若设2013年1月为第一个月,第x个月的利润为y万元;由于污染问题,该厂决定从2013年1月底适当限产,并投入资金进行新技术改造,导致月利润明显下降.从1月底到5月,y与x成反比例关系.到5月底,新技术改造任务顺利完成,从这时起,该厂每月利润比前月增加20万元(如图).
我省某化工厂2013年1月的利润为200万元,若设2013年1月为第一个月,第x个月的利润为y万元;由于污染问题,该厂决定从2013年1月底适当限产,并投入资金进行新技术改造,导致月利润明显下降.从1月底到5月,y与x成反比例关系.到5月底,新技术改造任务顺利完成,从这时起,该厂每月利润比前月增加20万元(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com