
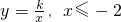 和x≥1的一部分图象,且其图象过(2,1)点,若二次
和x≥1的一部分图象,且其图象过(2,1)点,若二次 函数y=ax2的图象与上述图象有公共点,则a的取值范围为
函数y=ax2的图象与上述图象有公共点,则a的取值范围为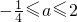 且a≠0
且a≠0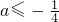 或a≥2
或a≥2 的图象过(2,1)点,即可求得反比例函数的解析式,继而可得反比例函数过点(1,2),(-2,-1),又由二次函数y=ax2的图象与反比例函数图象有公共点,即可从当a>0时,a的最大值即是过点(1,2)时的取值与当a<0时,a的最小值即是过点(-2,-1)时的取值,即可求得答案.
的图象过(2,1)点,即可求得反比例函数的解析式,继而可得反比例函数过点(1,2),(-2,-1),又由二次函数y=ax2的图象与反比例函数图象有公共点,即可从当a>0时,a的最大值即是过点(1,2)时的取值与当a<0时,a的最小值即是过点(-2,-1)时的取值,即可求得答案. 的图象过(2,1)点,
的图象过(2,1)点, ,
, ,
, ≤a<0;
≤a<0; ≤a≤2且a≠0.
≤a≤2且a≠0.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源:2008年安徽省马鞍山市第二中学理科实验班招生数学试卷(解析版) 题型:选择题
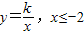 和x≥1的一部分图象,且其图象过(2,1)点,若二次函数y=ax2的图象与上述图象有公共点,则a的取值范围为( )
和x≥1的一部分图象,且其图象过(2,1)点,若二次函数y=ax2的图象与上述图象有公共点,则a的取值范围为( )
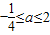 且a≠0
且a≠0 或a≥2
或a≥2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com