
【题目】 九⑴班![]() 名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下
名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下![]() 名学生成绩尚未统计,这
名学生成绩尚未统计,这![]() 名学生成绩如下:
名学生成绩如下:![]() .
.
频数分布表
分数段 | 频数(人数) |
|
|
|
|
|
|
|
|

请解答下列问题:
⑴完成频数分布表,![]() ,
,![]() .
.
⑵补全频数分布直方图;
⑶全校共有![]() 名学生参加初赛,估计该校成绩
名学生参加初赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?
⑷九⑴班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
【答案】(1)4,4;(2)见解析;(3)50;(4)![]() .
.
【解析】
试题分析:(1)将余下的8位同学按60≤x<70、90≤x<100分组可得a、b的值;
(2)根据(1)中所得结果补全即可得;
(3)将样本中成绩90≤x<100范围内的学生所占比例乘以总人数600可得答案;
(4)画树状图列出所有等可能结果,根据概率公式求解可得.
试题解析:(1)由题意知,60≤x<70的有60、63、67、68这4个数,90≤x<100的有90、99、99、99这4个,即a=4、b=4,
故答案为4,4;
(2)补全频数分布直方图如下:
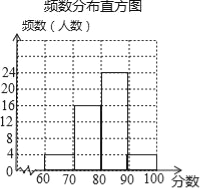
(3)600×![]() =50(人),故答案为:估计该校成绩90≤x<100范围内的学生有50人.
=50(人),故答案为:估计该校成绩90≤x<100范围内的学生有50人.
(4)画树状图得:
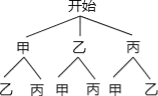
∵共有6种等可能的结果,甲、乙被选中的有2种情况,
∴甲、乙被选中的概率为![]() ..
..


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F. 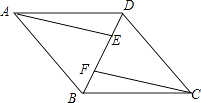
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3经过点A(1,0)和点B(5,0).
(1)求该抛物线所对应的函数解析式;
(2)该抛物线与直线![]() 相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.
相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.
①连结PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
②连结PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个容量为16GB的便携式U盘的内存全部用来储数码照片,若每张照片文件大小为211KB,则这个U盘可以存储这样的数码照片张.(16GB=224KB,用2为底的幂表示结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
数学课上,老师让同学们解答课本中的习题:如图1,在四边形ABCD中,E、F、
G、H分别是各边的中点,猜想四边形EFGH的形状并证明自己的猜想.
小丽在思考问题时,有如下思路:连接AC
结合小丽的思路作答:
(1)若只改变图1中的四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?请说明理由
参考小丽思考问题方法,解决以下问题:
(2)如图2,在(1)的条件下,若连接AC、BD
①当AC与BD满足什么关系时,四边形EFGH是菱形.写出结论并证明.
②当AC与BD满足什么关系时,四边形EFGH是正方形.直接写出结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() ,
,![]() ,
,![]() 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称![]() ,
,![]() ,
,![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() ,
,![]() ,
,![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com