

 ,所形成的图形的周长为4a.
,所形成的图形的周长为4a.| 第1次 生长后 | 第2次 生长后 | 第3次 生长后 | … | 第n次 生长后 | |
| 每个小等边 三角形的边长 |  | ________ | ________ | … | ________ |
| 所形成的 图形的周长 | 4a | ________ | ________ | … | ________ |
 a
a 
 a 3a(
a 3a( )2 3a(
)2 3a( )3 3a(
)3 3a( )n
)n ,以此类推,即可得到第4次变换后得到的图形的周长.边长变为原来的
,以此类推,即可得到第4次变换后得到的图形的周长.边长变为原来的 .
. ,
, a;
a; ×
× a=
a= a;
a; ×
× ×
× =
= a
a a;
a; =4a
=4a ×
× ,
, ×
× ×
× ,
, )n.
)n.

 …
… a所形成的
a所形成的 3a(
3a( )3…3a(
)3…3a( )n
)n ,是解答本题的关键.
,是解答本题的关键. 

科目:初中数学 来源: 题型:
 20、如图,把一个等边三角形进行分割,第一步从图(1)到图(2),一个三角形分为4个三角形;第二步从图(2)到图(3),将4个三角形分为13个三角形.按这个规律分割下去,第3步分割完成后共有
20、如图,把一个等边三角形进行分割,第一步从图(1)到图(2),一个三角形分为4个三角形;第二步从图(2)到图(3),将4个三角形分为13个三角形.按这个规律分割下去,第3步分割完成后共有查看答案和解析>>
科目:初中数学 来源: 题型:
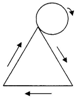 (2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了
(2012•深圳模拟)如图一个等边三角形的边长与它的一边相外切的圆的周长相等,当这个圆按箭头方向从某一位置沿等边三角形的三边做无滑动旋转,直至回到原出发位置时,则这个圆共转了查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
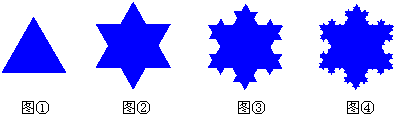
| 1 |
| 3 |
| 第1次 生长后 |
第2次 生长后 |
第3次 生长后 |
… | 第n次 生长后 | |||
| 每个小等边 三角形的边长 |
|
… | |||||
| 所形成的 图形的周长 |
4a | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com