
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

【答案】(1)见解析(2)成立(3)△DEF为等边三角形
【解析】解:(1) 证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=900。
∵∠BAC=900,∴∠BAD+∠CAE=900。
∵∠BAD+∠ABD=900,∴∠CAE=∠ABD。
又AB=AC ,∴△ADB≌△CEA(AAS)。∴AE=BD,AD=CE。
∴DE=AE+AD= BD+CE。
(2)成立。证明如下:
∵∠BDA =∠BAC=![]() ,∴∠DBA+∠BAD=∠BAD +∠CAE=1800—
,∴∠DBA+∠BAD=∠BAD +∠CAE=1800—![]() 。∴∠DBA=∠CAE。
。∴∠DBA=∠CAE。
∵∠BDA=∠AEC=![]() ,AB=AC,∴△ADB≌△CEA(AAS)。∴AE=BD,AD=CE。
,AB=AC,∴△ADB≌△CEA(AAS)。∴AE=BD,AD=CE。
∴DE=AE+AD=BD+CE。
(3)△DEF为等边三角形。理由如下:
由(2)知,△ADB≌△CEA,BD=AE,∠DBA =∠CAE,
∵△ABF和△ACF均为等边三角形,∴∠ABF=∠CAF=600。
∴∠DBA+∠ABF=∠CAE+∠CAF。∴∠DBF=∠FAE。
∵BF=AF,∴△DBF≌△EAF(AAS)。∴DF=EF,∠BFD=∠AFE。
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600。
∴△DEF为等边三角形。
(1)因为DE=DA+AE,故由AAS证△ADB≌△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE。
(2)成立,仍然通过证明△ADB≌△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD。
(3)由△ADB≌△CEA得BD=AE,∠DBA =∠CAE,由△ABF和△ACF均等边三角形,得∠ABF=∠CAF=600,FB=FA,所以∠DBA+∠ABF=∠CAE+∠CAF,即∠DBF=∠FAE,所以△DBF≌△EAF,所以FD=FE,∠BFD=∠AFE,再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF是等边三角形。


科目:初中数学 来源: 题型:
【题目】如图,这是一个“数值转换机”(箭头为数进入转换机的路径,方框是对进入的数进行转换的转换机).
(1)当输入7、-2018这两个数时,求出它们各自输出的结果;

(2)若输入一非零数,其输出结果为0,则输入的数是多少?(找一个即可)
(3)若输出的结果是2,请直接写出输入的数.(用含自然数n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在河的两岸有A,B两个村庄,河宽为4千米,A、B两村庄的直线距离 AB=10千米,A、B两村庄到河岸的距离分别为1千米、3千米,计划在河上修建一座桥MN垂直于两岸,M点为靠近A村庄的河岸上一点,求AM+BN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
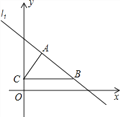
【题目】如图,在平面直角坐标系中,直线![]() 经过第一象限的点
经过第一象限的点![]() 和点
和点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 的面积为
的面积为![]() .
.
![]() 求
求![]() 点的坐标;
点的坐标;
![]() 求直线
求直线![]() 的函数表达式;
的函数表达式;
![]() 直线
直线![]() 经过线段
经过线段![]() 上一点
上一点![]() (
(![]() 不与
不与![]() 、
、![]() 重合),求
重合),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过 秒钟两人第一次相遇;若两人同时出发,同向而行,则经过 秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本期开学以来,初2015级开展了轰轰烈烈的体育锻炼,为了解考体育科目训练的效果,九年级学生中随机抽取了部分学生进行了以此中考体育科目测试(把测试结果分为四个等级,A等:优秀;B等:良好;C等:及格;D等:不及格),并将结果汇成了如图1、2所示两幅不同统计图,请根据统计图中的信息解答下列问题: 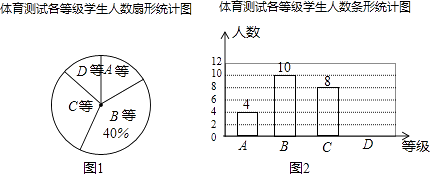
(1)本次抽样测试的学生人数是;
(2)图1扇形图中D等所在的扇形的圆心角的度数是 , 并把图2条形统计图补充完整;
(3)我校九年级有1800名学生,如果全部参加这次中考体育科目测试,请估计不及格的人数为;
(4)已知得A等的同学有一位男生,体育老师想从4为同学中随机选择两位同学向其他同学介绍经验,请用列表法或画树形图的方法求出选中的两人刚好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
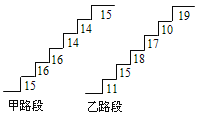
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com