
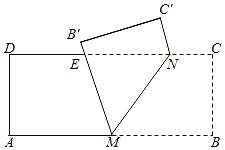
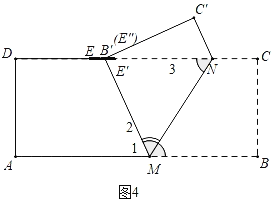
【题目】如图,有一张矩形纸条ABCD,AB=5cm,BC=2cm,点M,N分别在边AB,CD上,CN=1cm.现将四边形BCNM沿MN折叠,使点B,C分别落在点B',C'上.当点B'恰好落在边CD上时,线段BM的长为_____cm;在点M从点A运动到点B的过程中,若边MB'与边CD交于点E,则点E相应运动的路径长为_____cm.
【答案】![]()
![]()
【解析】
第一个问题证明BM=MB′=NB′,求出NB即可解决问题.第二个问题,探究点E的运动轨迹,寻找特殊位置解决问题即可.
如图1中,
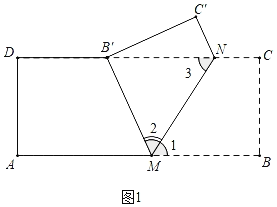
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠1=∠3,
由翻折的性质可知:∠1=∠2,BM=MB′,
∴∠2=∠3,
∴MB′=NB′,
∵NB′=![]() =
=![]() =
=![]() (cm),
(cm),
∴BM=NB′=![]() (cm).
(cm).
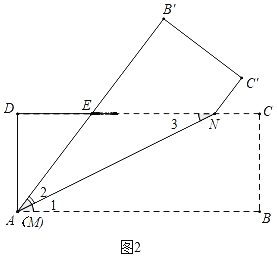
如图2中,当点M与A重合时,AE=EN,设AE=EN=xcm,
在Rt△ADE中,则有x2=22+(4﹣x)2,解得x=![]() ,
,
∴DE=4﹣![]() =
=![]() (cm),
(cm),
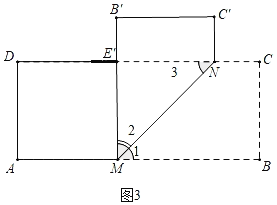
如图3中,当点M运动到MB′⊥AB时,DE′的值最大,DE′=5﹣1﹣2=2(cm),
如图4中,当点M运动到点B′落在CD时,DB′(即DE″)=5﹣1﹣![]() =(4﹣
=(4﹣![]() )(cm),
)(cm),
∴点E的运动轨迹E→E′→E″,运动路径=EE′+E′B′=2﹣![]() +2﹣(4﹣
+2﹣(4﹣![]() )=(
)=(![]() )(cm).
)(cm).
故答案为![]() ,(
,(![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与y轴交于点C,与反比例函数y=![]() (k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
(k≠0)的图象交于A,B两点,点A在第一象限,纵坐标为4,点B在第三象限,BM⊥x轴,垂足为点M,BM=OM=2.
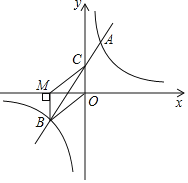
(1)求反比例函数和一次函数的解析式.
(2)连接OB,MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形具有不稳定性,对于四条边长确定的四边形.当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′.若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
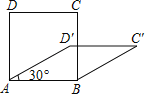
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业承接了27000件产品的生产任务,计划安排甲、乙两个车间的共50名工人,合作生产20天完成.已知甲、乙两个车间利用现有设备,工人的工作效率为:甲车间每人每天生产25件,乙车间每人每天生产30件.
(1)求甲、乙两个车间各有多少名工人参与生产?
(2)为了提前完成生产任务,该企业设计了两种方案:
方案一 甲车间租用先进生产设备,工人的工作效率可提高20%,乙车间维持不变.
方案二 乙车间再临时招聘若干名工人(工作效率与原工人相同),甲车间维持不变.
设计的这两种方案,企业完成生产任务的时间相同.
①求乙车间需临时招聘的工人数;
②若甲车间租用设备的租金每天900元,租用期间另需一次性支付运输等费用1500元;乙车间需支付临时招聘的工人每人每天200元.问:从新增加的费用考虑,应选择哪种方案能更节省开支?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点B.
(1)求该抛物线的函数表达式.
(2)当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m.
①求OD的长.
②东东抢到球后,因遭对方防守无法投篮,他在点D处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点E(4,1.3).东东起跳后所持球离地面高度h1(m)(传球前)与东东起跳后时间t(s)满足函数关系式h1=﹣2(t﹣0.5)2+2.7(0≤t≤1);小戴在点F(1.5,0)处拦截,他比东东晚0.3s垂直起跳,其拦截高度h2(m)与东东起跳后时间t(s)的函数关系如图2所示(其中两条抛物线的形状相同).东东的直线传球能否越过小戴的拦截传到点E?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计).
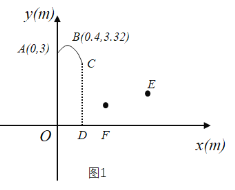

查看答案和解析>>
科目:初中数学 来源: 题型:
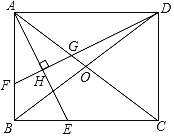
【题目】(性质探究)
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE平分∠BAC,交BC于点E.作DF⊥AE于点H,分别交AB,AC于点F,G.
(1)判断△AFG的形状并说明理由.
(2)求证:BF=2OG.
(迁移应用)
(3)记△DGO的面积为S1,△DBF的面积为S2,当![]() 时,求
时,求![]() 的值.
的值.
(拓展延伸)
(4)若DF交射线AB于点F,(性质探究)中的其余条件不变,连结EF,当△BEF的面积为矩形ABCD面积的![]() 时,请直接写出tan∠BAE的值.
时,请直接写出tan∠BAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
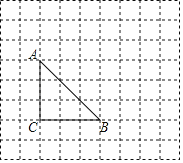
【题目】如图,在由边长为1个单位长度的小正方形组成的8×9的网格中,已知△ABC的顶点均为网格线的交点.
(1)在给定的网格中,画出△ABC关于直线AB对称的△ABC1.
(2)将△ABC1绕着点O旋转后能与△ABC重合,请在网格中画出点O的位置.
(3)在给定的网格中,画出以点C为位似中心,将△ABC放大为原来的2倍后得到的△A2B2C.
查看答案和解析>>
科目:初中数学 来源: 题型:
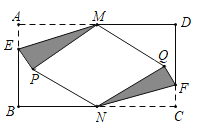
【题目】如图, 在矩形纸片![]() 中,
中, ![]() , 点
, 点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点, 点
的中点, 点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上, 且
上, 且![]() .将
.将![]() 沿
沿![]() 折叠, 点
折叠, 点![]() 的对应点为点
的对应点为点![]() ,将
,将![]() 沿
沿![]() 折叠, 点
折叠, 点![]() 的对应点为点
的对应点为点![]() ,当四边形
,当四边形![]() 为菱形时, 则
为菱形时, 则![]() _______.
_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com