
小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量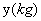 与上市时间
与上市时间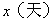 的函数关系如图1所示,樱桃价格
的函数关系如图1所示,樱桃价格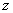 (元/
(元/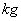 )与上市时间
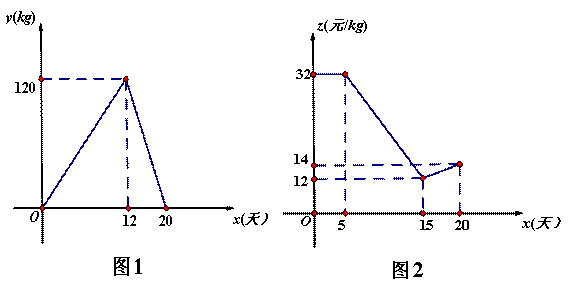
)与上市时间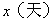 的函数关系式如图2所示。
的函数关系式如图2所示。
 |
(1)求小明家樱桃的日销售量y与上市时间x的函数解析式。
(2)求当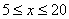 时,樱桃的价格z与上市时间x的函数解析式。
时,樱桃的价格z与上市时间x的函数解析式。
(3)求哪一天的销售金额达到最大,最大值是多少?
解:(1)把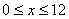 和
和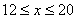 的函数解析式分别设为
的函数解析式分别设为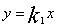 和
和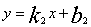
把(12,120)代入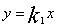 ,得
,得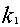 =10,即
=10,即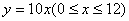 。。。。。。。2分
。。。。。。。2分
把(12,120)和(20,0)分别代入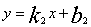
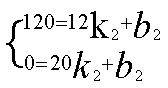 得
得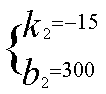
∴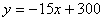 (
(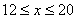 )。。。。。。。。。。。。。。。。。。。。2分
)。。。。。。。。。。。。。。。。。。。。2分
(2)设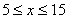 时,
时,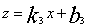
把(5,32)和(15,12)分别代入
得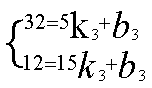 解得
解得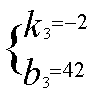
∴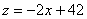 (
(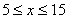 )。。。。。。。。。。。。。。。。。。。。。。。2分
)。。。。。。。。。。。。。。。。。。。。。。。2分
设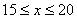 时,
时,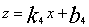
把(15,12)和(20,14)分别代入
得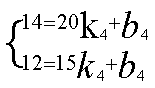 解得
解得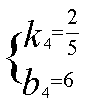
∴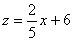 (
(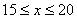 )。。。。。。。。。。。。。。。。。。。。。。。。2分
)。。。。。。。。。。。。。。。。。。。。。。。。2分
(3)设每天樱桃的销售金额为w。则w=zy。
由题意得,当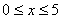 时,w=32×10x,所以当x=5时,
时,w=32×10x,所以当x=5时,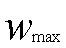 =1600元
=1600元
当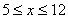 时,w=(-2x+42)×10x,当
时,w=(-2x+42)×10x,当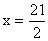 时,有最大值,但x取整数,所以当x=10时,W=2200,当x=11时,W=2200,所以
时,有最大值,但x取整数,所以当x=10时,W=2200,当x=11时,W=2200,所以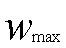 =2200元
=2200元
当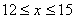 时,w=(-2x+42)×(-15x+300),当x=12时,
时,w=(-2x+42)×(-15x+300),当x=12时,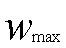 =2160元
=2160元
当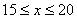 时,w=
时,w=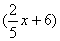 ×(-15x+300),当x=15时,
×(-15x+300),当x=15时,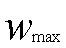 =900元
=900元
综上所述,在第10天或11天时,每天的销售金额最大,最大值为2200元。。。。4分


科目:初中数学 来源: 题型:
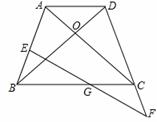
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF 交BC于G,请判断G点是否为EF中点,并说明理由. (改编)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知直线AC: 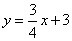 与直线BC:
与直线BC: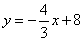 相交于点C,分别交x轴于点A、B,P为x轴上的一点,设P(m,0),以点P为圆心作圆:
相交于点C,分别交x轴于点A、B,P为x轴上的一点,设P(m,0),以点P为圆心作圆:
(1)若-4<m <6.当m=______时,⊙P同时与AC、BC相切;
(2)设⊙P的半径为3,当m=_______时,⊙P与直线AC、直线BC中的一条相切。
查看答案和解析>>
科目:初中数学 来源: 题型:
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C( ,3),规定M={Y1,Y2,Y3中最小的函数值}
,3),规定M={Y1,Y2,Y3中最小的函数值}
则下列结论错误的是( )
A.当 时,M=Y1
时,M=Y1
B.当 时,Y2
时,Y2 Y3
Y3 Y1
Y1
C.当0≤ ≤2时,M的最大值是1,无最小值
≤2时,M的最大值是1,无最小值
D.当 ≥2时,M最大值是1,无最小值
≥2时,M最大值是1,无最小值
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
数学活动﹣求重叠部分的面积
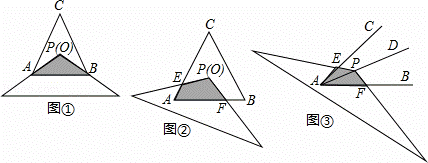
(1)问题情境:如图①,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点P与等边△ABC的内心O重合,已知OA=2,则图中重叠部分△PAB的面积为 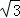 .
.
(2)探究1:在(1)的条件下,将纸片绕P点旋转至如图②所示位置,纸片两边分别与AC,AB交于点E,F,图②中重叠部分的面积与图①重叠部分的面积是否相等?如果相等,请给予证明;如果不相等,请说明理由.
(3)探究2:如图③,若∠CAB=α(0°<α<90°),AD为∠CAB的角平分线,点P在射线AD上,且AP=2,以P为顶点的等腰三角形纸片(纸片足够大)与∠CAB的两边AC,AB分别交于点E、F,∠EPF=180°﹣α,求重叠部分的面积.(用α或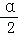 的三角函数值表示)
的三角函数值表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com