
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
;(3)当t为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
【解析】
试题(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)设出发![]() 秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=
秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=![]() ,BP=
,BP=![]() ,列式求得
,列式求得![]() 即可;
即可;
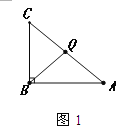
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:①当CQ=BQ时(图1),则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得![]() ;
;
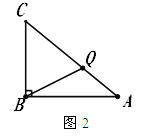
②当CQ=BC时(如图2),则BC+CQ=12,易求得![]() ;
;
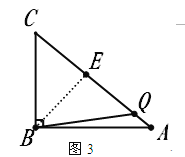
③当BC=BQ时(如图3),过B点作BE⊥AC于点E,则求出BE,CE,即可得出![]() .
.
试题解析:(1)BQ=2×2=4cm,BP=AB﹣AP=8﹣2×1=6cm,∵∠B=90°,
PQ=![]() ;
;
(2)BQ=![]() ,BP=
,BP=![]() ,
,![]() ,解得:
,解得:![]() ;
;
(3)①当CQ=BQ时(图1),则∠C=∠CBQ,∵∠ABC=90°,∴∠CBQ+∠ABQ=90°,∠A+∠C=90°,∴∠A=∠ABQ,∴BQ=AQ,∴CQ=AQ=5,∴BC+CQ=11,∴![]() =11÷2=5.5秒.
=11÷2=5.5秒.
②当CQ=BC时(如图2),则BC+CQ=12,∴![]() =12÷2=6秒.
=12÷2=6秒.
③当BC=BQ时(如图3),过B点作BE⊥AC于点E,则BE=![]() ,所以CE=
,所以CE=![]() ,故CQ=2CE=7.2,所以BC+CQ=13.2,∴
,故CQ=2CE=7.2,所以BC+CQ=13.2,∴![]() =13.2÷2=6.6秒.
=13.2÷2=6.6秒.
由上可知,当![]() 为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.
为5.5秒或6秒或6.6秒时,△BCQ为等腰三角形.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.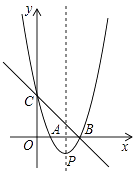
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3000米.甲同学先步行600米,然后乘公交车去学校、乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
,公交车的速度是乙骑自行车速度的2倍.甲乙两同学同时从家发去学校,结果甲同学比乙同学早到2分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
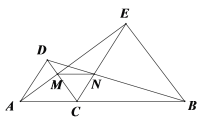
【题目】如图,点C在AB上,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,则下列结论:①AE=DB;②CM=CN;③△CMN为等边三角形;④MN//BC;
正确的有_________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题学习:我们知道二次函数的图象是抛物线,它也可以这样定义:如果一个动点M(x,y)到定点A(0,m)(m>0)的距离与它到定直线y=﹣m的距离相等,那么动点M形成的图形就是抛物线y=ax2(a>0)的图象,如图所示.
(1)探究:当x≠0时,a与m有何数量关系?
(2)应用:已知动点M(x,y)到定点A(0,4)的距离与到定直线y=﹣4的距离相等,请写出动点M形成的抛物线的解析式.
(3)拓展:根据抛物线的平移变换,抛物线y= ![]() (x﹣1)2+2的图象可以看作到定点A( , )的距离与它到定直线y=的距离相等的动点M(x,y)所形成的图形.
(x﹣1)2+2的图象可以看作到定点A( , )的距离与它到定直线y=的距离相等的动点M(x,y)所形成的图形.
(4)若点D的坐标是(1,8),在(2)中求得的抛物线上是否存在点P,使得PA+PD最短?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等边三角形.
(1)如图,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F.试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com