已知抛物线y=mx2-(m-5)x-5(m>0),与x轴交于两点A(x1,0),B(x2,0),(x1<x2),与y轴交于点C且AB=6.
(1)求抛物线的解析式;
(2)若⊙M过A、B、C三点,求⊙M的半径,并求M到直线BC的距离;
(3)抛物线上是否存在点P,过点P作PQ⊥x轴于点Q,使△PBQ被直线BC分成面积相等的两部分,若存在,求出P点的坐标;若不存在,请说明理由.
分析:(1)根据抛物线的解析式,可求出A、B点的坐标,根据AB=6,即可求出m的值,由此确定抛物线的解析式;
(2)由于圆心同时经过A、B,则圆心必在抛物线的对称轴上,由此可得到点M的横坐标,设出M点的纵坐标,B、C的坐标易求得,可用平面直角坐标系中两点间的距离公式求出MB
2、MC
2的长,由于MB、MC都是⊙M的半径,则上面所得两条线段平方的表达式相等,由此可求出M点的坐标,进而可求出⊙M的半径,而M到直线BC的距离可由勾股定理和垂径定理求得;
(3)假设存在符合条件的P点,设PQ与直线BC的交点为H,如果BC将△PBQ分成面积相等的两部分,那么QH=PH=
PQ(△BHQ、△BPH同高,若面积相等则底边相等),可先求出直线BC的解析式,设出P点横坐标,根据直线BC和抛物线的解析式表示出H、P的纵坐标,从而得到QH、PQ的长,再根据QH、PQ的数量关系列方程求出点P的坐标.
解答:解:(1)y=mx
2-(m-5)x-5(m>0)
=(x-1)(mx+5)=m(x-1)(x+
);
∴x
1=-
,x
2=1;
∴|AB|=1+
=6,m=1;
∴y=x
2+4x-5;A(-5,0),B(1,0),C(0,-5);
(2)圆心M的坐标为(-2,x),且MB=MC;
(-2-1)
2+x
2=4+(x+5)
2,x=-2;
设⊙M的半径为r,
∴r
2=x
2+9=4+9=13;
∴r=
,BC=
;
∴d=
=
=
;
(3)假设存在点P(x
P,y
P),
∵P在抛物线上,
∴y
P=x
P2+4x
P-5,Q(x
P,0);
∵直线BC的方程为y=5x-5,而直线PQ的方程为x=x
P,
∴设BC与PQ的交点为H,H(x
P,5x
P-5);
∴
=,
∴
=
;
∴x
P=1(舍去)或x
P=5;
∴存在点P(5,40).
点评:此题主要考查了二次函数与坐标轴交点坐标的求法、二次函数解析式的确定、勾股定理、垂径定理的应用、三角形面积的求法等重要知识点,综合性强,难度较大.



 备战中考寒假系列答案
备战中考寒假系列答案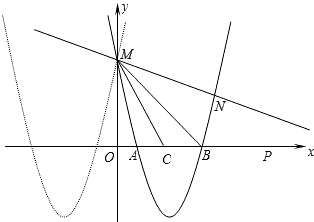 点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为
点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为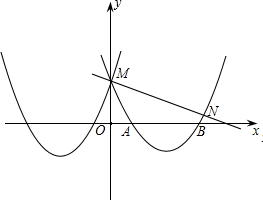 点M,与x轴交于点A和B.
点M,与x轴交于点A和B. 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.