
·ÖÎö £¨1£©ÏÈÀûÓûýµÄ³Ë·½µÃµ½Ôʽ=[£¨$\sqrt{3}$-$\sqrt{2}$£©£¨$\sqrt{3}$+$\sqrt{2}$£©]2014•£¨$\sqrt{3}$+$\sqrt{2}$£©£¬È»ºóÀûÓÃƽ·½²î¹«Ê½¼ÆË㣻
£¨2£©ÏȰѸ÷¶þ´Î¸ùʽ»¯¼òΪ×î¼ò¶þ´Î¸ùʽ£¬È»ºóºÏ²¢¼´¿É£»
£¨3£©ÏȽøÐжþ´Î¸ùʽµÄ³ý·¨ÔËË㣬Ȼºó°Ñ¸÷¶þ´Î¸ùʽ»¯¼òΪ×î¼ò¶þ´Î¸ùʽºóºÏ²¢¼´¿É£»
£¨4£©¸ù¾ÝÁãÖ¸ÊýÃݵÄÒâÒåºÍ¸ºÕûÊýÃݵÄÒâÒå¼ÆË㣮
½â´ð ½â£º£¨1£©Ôʽ=[£¨$\sqrt{3}$-$\sqrt{2}$£©£¨$\sqrt{3}$+$\sqrt{2}$£©]2014•£¨$\sqrt{3}$+$\sqrt{2}$£©
=£¨3-2£©2014•£¨$\sqrt{3}$+$\sqrt{2}$£©
=$\sqrt{3}$+$\sqrt{2}$£»
£¨2£©Ôʽ=4$\sqrt{2}$-5$\sqrt{3}$-$\frac{\sqrt{2}}{2}$-$\frac{2\sqrt{3}}{3}$
=$\frac{7\sqrt{2}}{2}$-$\frac{17\sqrt{3}}{3}$£»
£¨3£©Ôʽ=2$\sqrt{3}$+2$\sqrt{\frac{1}{2}¡Á\frac{1}{2}}$+$\frac{3}{2}$$\sqrt{4}$
=2$\sqrt{3}$-1+3
=2$\sqrt{3}$+2£»
£¨4£©Ôʽ=2$\sqrt{3}$-1+2+$\sqrt{3}$-1
=3$\sqrt{3}$£®
µãÆÀ ±¾Ì⿼²éÁ˶þ´Î¸ùʽµÄ»ìºÏÔËË㣺ÏȰѸ÷¶þ´Î¸ùʽ»¯¼òΪ×î¼ò¶þ´Î¸ùʽ£¬È»ºó½øÐжþ´Î¸ùʽµÄ³Ë³ýÔËË㣬Ôٺϲ¢¼´¿É£®



| Ä꼶 | ¸ßÖÐ¿Î³Ì | Ä꼶 | ³õÖÐ¿Î³Ì |
| ¸ßÒ» | ¸ßÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ | ³õÒ» | ³õÒ»Ãâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ß¶þ | ¸ß¶þÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õ¶þ | ³õ¶þÃâ·Ñ¿Î³ÌÍƼö£¡ |
| ¸ßÈý | ¸ßÈýÃâ·Ñ¿Î³ÌÍƼö£¡ | ³õÈý | ³õÈýÃâ·Ñ¿Î³ÌÍƼö£¡ |
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | Õý·½ÐÎ | B£® | µÈ±ßÈý½ÇÐÎ | C£® | ³¤·½ÐÎ | D£® | ƽÐÐËıßÐÎ |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
 С´ÏºÍСÃ÷ÑØͬһÌõ·ͬʱ´ÓѧУ³ö·¢µ½Ä³³¬ÊйºÎѧУÓ볬ÊеÄ·³ÌÊÇ4ǧÃ×£®Ð¡´ÏÆï×ÔÐгµ£¬Ð¡Ã÷²½ÐУ¬µ±Ð¡´Ï´ÓÔ·»Øµ½Ñ§Ð£Ê±£¬Ð¡Ã÷¸ÕºÃµ½´ï³¬ÊУ®Í¼ÖÐÕÛÏßO-A-B-CºÍÏ߶ÎOD·Ö±ð±íʾÁ½ÈËÀëѧУµÄ·³Ìs£¨Ç§Ã×£©ÓëËù¾¹ýµÄʱ¼ät£¨·ÖÖÓ£©Ö®¼äµÄº¯Êý¹Øϵ£¬Çë¸ù¾ÝͼÏó»Ø´ðÏÂÁÐÎÊÌ⣺
С´ÏºÍСÃ÷ÑØͬһÌõ·ͬʱ´ÓѧУ³ö·¢µ½Ä³³¬ÊйºÎѧУÓ볬ÊеÄ·³ÌÊÇ4ǧÃ×£®Ð¡´ÏÆï×ÔÐгµ£¬Ð¡Ã÷²½ÐУ¬µ±Ð¡´Ï´ÓÔ·»Øµ½Ñ§Ð£Ê±£¬Ð¡Ã÷¸ÕºÃµ½´ï³¬ÊУ®Í¼ÖÐÕÛÏßO-A-B-CºÍÏ߶ÎOD·Ö±ð±íʾÁ½ÈËÀëѧУµÄ·³Ìs£¨Ç§Ã×£©ÓëËù¾¹ýµÄʱ¼ät£¨·ÖÖÓ£©Ö®¼äµÄº¯Êý¹Øϵ£¬Çë¸ù¾ÝͼÏó»Ø´ðÏÂÁÐÎÊÌ⣺²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£ºÑ¡ÔñÌâ
| A£® | £¨x-3£©2=2 | B£® | 325x2-326x+1=0 | C£® | x2-100x+2500=0 | D£® | 2x2+3x-1=0 |
²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
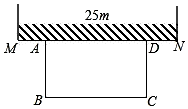 Èçͼ£¬Ä³Å©³¡ÀÏ°å×¼±¸½¨ÔìÒ»¸ö¾ØÐÎÑòȦABCD£¬Ëû´òËãÈþØÐÎÑòȦµÄÒ»ÃæÍêÈ«¿¿×ÅǽMN£¬Ç½MN¿ÉÀûÓõij¤¶ÈΪ25m£¬ÁíÍâÈýÃæÓó¤¶ÈΪ50mµÄÀé°ÊΧ³É£¨Àé°ÊÕýºÃҪȫ²¿ÓÃÍ꣬ÇÒ²»¿¼ÂǽÓÍ·µÄ²¿·Ö£©£¬Éè¾ØÐÎÑòȦµÄÃæ»ýΪym2£¬´¹Ö±ÓÚǽµÄÒ»±ß³¤ABΪx m£®
Èçͼ£¬Ä³Å©³¡ÀÏ°å×¼±¸½¨ÔìÒ»¸ö¾ØÐÎÑòȦABCD£¬Ëû´òËãÈþØÐÎÑòȦµÄÒ»ÃæÍêÈ«¿¿×ÅǽMN£¬Ç½MN¿ÉÀûÓõij¤¶ÈΪ25m£¬ÁíÍâÈýÃæÓó¤¶ÈΪ50mµÄÀé°ÊΧ³É£¨Àé°ÊÕýºÃҪȫ²¿ÓÃÍ꣬ÇÒ²»¿¼ÂǽÓÍ·µÄ²¿·Ö£©£¬Éè¾ØÐÎÑòȦµÄÃæ»ýΪym2£¬´¹Ö±ÓÚǽµÄÒ»±ß³¤ABΪx m£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
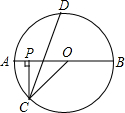 Èçͼ£¬PÊÇ¡ÑOµÄÖ±¾¶ABÉϵÄÒ»µã£¬PC¡ÍAB£¬PC½»¡ÑOÓÚC£¬¡ÏOCPµÄƽ·ÖÏß½»¡ÑOÓÚD£¬ÇóÖ¤£º$\widehat{AD}$=$\widehat{BD}$£®
Èçͼ£¬PÊÇ¡ÑOµÄÖ±¾¶ABÉϵÄÒ»µã£¬PC¡ÍAB£¬PC½»¡ÑOÓÚC£¬¡ÏOCPµÄƽ·ÖÏß½»¡ÑOÓÚD£¬ÇóÖ¤£º$\widehat{AD}$=$\widehat{BD}$£®²é¿´´ð°¸ºÍ½âÎö>>
¿ÆÄ¿£º³õÖÐÊýѧ À´Ô´£º ÌâÐÍ£º½â´ðÌâ
²é¿´´ð°¸ºÍ½âÎö>>
°Ù¶ÈÖÂÐÅ - Á·Ï°²áÁбí - ÊÔÌâÁбí
ºþ±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨Æ½Ì¨ | ÍøÉÏÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | µçÐÅթƾٱ¨×¨Çø | ÉæÀúÊ·ÐéÎÞÖ÷ÒåÓк¦ÐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ÐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com