
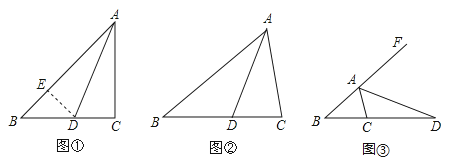
【题目】在△ABC中,∠ACB=2∠B,(1)如图①,当∠C=90°,AD为∠ABC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.请证明AB=AC+CD;
(2)①如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请直接写出你的结论,不要求证明;
②如图③,当∠C≠90°,AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明.
【答案】(1)证明见解析;(2)①AB=AC+CD;②AC+AB=CD,证明见解析.
【解析】
(1)首先得出△AED≌△ACD(SAS),即可得出∠B=∠BDE=45°,求出BE=DE=CD,进而得出答案;
(2)①首先得出△AED≌△ACD(SAS),即可得出∠B=∠BDE,求出BE=DE=CD,进而得出答案;
②首先得出△AED≌△ACD(SAS),即可得出∠B=∠EDC,求出BE=DE=CD,进而得出答案.
解:(1)∵AD为∠ABC的角平分线,
∴∠EAD=∠CAD,
在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,
∴△AED≌△ACD(SAS),
∴ED=CD,∠C=∠AED=90°,
∵∠ACB=2∠B,∠C=90°,
∴∠B=45°,∴∠BDE=45°,
∴BE=ED=CD,
∴AB=AE+BE=AC+CD;
(2)①AB=AC+CD.
理由:在AB上截取AE=AC,连接DE,
∵AD为∠ABC的角平分线,∴∠EAD=∠CAD,
在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,
∴△AED≌△ACD(SAS),
∴ED=CD,∠C=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
∵∠B+∠BDE=∠AED,
∴∠B=∠BDE,∴BE=ED=CD,
∴AB=AE+BE=AC+CD;
②AC+AB=CD.
理由:在射线BA上截取AE=AC,连接DE,
∵AD为∠EAC的角平分线,
∴∠EAD=∠CAD,
在△AED和△ACD中,∵AE=AC,∠EAD=∠CAD,AD=AD,
∴△AED≌△ACD(SAS),
∴ED=CD,∠ACD=∠AED,
∵∠ACB=2∠B,
∴设∠B=x,则∠ACB=2x,∴∠EAC=3x,∴∠EAD=∠CAD=1.5x,
∵∠ADC+∠CAD=∠ACB=2x,∴∠ADC=0.5x,∴∠EDC=x,
∴∠B=∠EDC,∴BE=ED=CD,
∴AB+AE=BE=AC+AB=CD.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,对角线AC和BD相交于点O,正方形A1B1C1O的边OA1交AB于点E,OC1交BC于点F,正方形A1B1C1O绕O点转动的过程中,与正方形ABCD重叠部分的面积为_____(用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.有两条边对应相等的两个三角形全等
B.两腰对应相等的两个等腰三角形全等
C.两角对应相等的两个等腰三角形全等
D.一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A.AB=DC,AD=BCB.AB∥DC,AD∥BC
C.AB∥DC,AD=BCD.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)如图2,直线BO与⊙O交于点D,E,若BD=4,AB=16,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应集合的括号内
+8.5, 0, -3.4, 12, -9, ![]() , 3.1415, -1.2,
, 3.1415, -1.2,![]() ,
, ![]()
(1)正数集合 { }
(2)整数集合 { }
(3)负分数集合 { }
(4)非正整数集合{ }
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com