
 分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
 x+2的交点坐标,据此即可求得m的范围;
x+2的交点坐标,据此即可求得m的范围; x+2的上面的部分到直线的距离的最大值,到直线y=
x+2的上面的部分到直线的距离的最大值,到直线y= x+2的距离最大的点,一定与直线平行且与抛物线只有一个公共点,可以设出直线的解析式,直线与抛物线组成的方程组只有一个解,利用判别式即可求解.两直线之间的距离就是最大值.
x+2的距离最大的点,一定与直线平行且与抛物线只有一个公共点,可以设出直线的解析式,直线与抛物线组成的方程组只有一个解,利用判别式即可求解.两直线之间的距离就是最大值. 中,令x=0,解得y=2,则OB=OD=2;
中,令x=0,解得y=2,则OB=OD=2; x+2=0,解得:x=-4,则OA=OC=4,故A的坐标是(-4,0),B的坐标是(0,2),C的坐标是:(0,4),D的坐标是:(2,0).
x+2=0,解得:x=-4,则OA=OC=4,故A的坐标是(-4,0),B的坐标是(0,2),C的坐标是:(0,4),D的坐标是:(2,0). ,
, .
. x2-x+4.
x2-x+4. =-1.
=-1. +1+4=
+1+4= ,则顶点坐标是:(-1,
,则顶点坐标是:(-1, ).
). x+2中,令x=-1,解得:y=
x+2中,令x=-1,解得:y= .
. -
- =3,因而m的范围是:3<m<
=3,因而m的范围是:3<m< .
.
 x+a,
x+a, x+a代入抛物线的解析式得:
x+a代入抛物线的解析式得: x+a=-
x+a=- x2-x+4,
x2-x+4, x2-
x2- x+4-a=0,
x+4-a=0, .
. x+
x+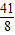 .
. x+2与y=
x+2与y= x+
x+ 之间与y轴的交点之间的距离是:
之间与y轴的交点之间的距离是: .
. ≤t<
≤t< .
.

科目:初中数学 来源: 题型:解答题
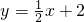 分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.
分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD. 抛物线y=ax2+bx+c经过A、C、D三点.
抛物线y=ax2+bx+c经过A、C、D三点.查看答案和解析>>
科目:初中数学 来源:2013年广西中考数学试卷(样卷)(解析版) 题型:解答题
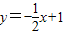 分别交y轴、x轴于A,B两点,以线段AB为边向上作正方形ABCD过点A,D,C的抛物线y=ax2+bx+1与直线的另一交点为点E
分别交y轴、x轴于A,B两点,以线段AB为边向上作正方形ABCD过点A,D,C的抛物线y=ax2+bx+1与直线的另一交点为点E 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
查看答案和解析>>
科目:初中数学 来源:2012年江苏省南通市中考数学二模试卷(解析版) 题型:解答题
 分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
分别交x轴、y轴于A、B两点,将△OAB绕坐标原点O顺时针旋转90°得到△OCD.抛物线y=ax2+bx+c经过A、C、D三点.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南省扶沟县初三下学期《解直角三角形》检测题 题型:选择题
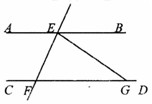
如图,已知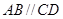 ,直线
,直线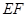 分别交
分别交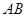 、
、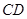 于点
于点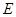 、
、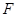 ,过
,过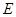 作
作 于点
于点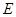 ,交
,交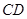 于点
于点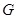 。若
。若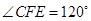 ,则
,则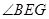 的大小为( )
的大小为( )
A.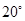 B.
B.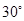 C.
C.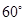 D.
D.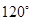
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com