
分析 (1)根据高铁的行驶路程是400千米和普通列车的行驶路程是高铁的行驶路程的1.3倍,两数相乘即可得出答案;
(2)设普通列车平均速度是x千米/时,根据高铁所需时间比乘坐普通列车所需时间缩短3小时,列出分式方程,然后求解即可;
解答 解:(1)依题意可得,普通列车的行驶里程为:400×1.3=520(千米).
(2)设普通列车的平均速度为x千米/时,则高铁的平均速度为2.5x千米/时,
根据题题得:$\frac{520}{x}-\frac{400}{2.5x}=3$,
解之得:x=120,
经检验x=120是原方程的解,
所以原方程的解为x=120;
所以高铁的平均速度为2.5×120=300(千米/时);
答:高铁的平均速度为300千米/时.
点评 此题考查了分式方程的应用,关键是分析题意,找到合适的数量关系列出方程,解分式方程时要注意检验.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
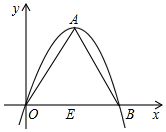 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
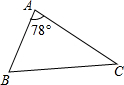 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )| A. | 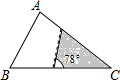 | B. |  | C. | 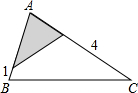 | D. | 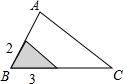 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{7}$+3=$\frac{x}{9}$-3 | B. | $\frac{x}{7}$-3=$\frac{x}{9}$+3 | C. | $\frac{x}{7}$+3=$\frac{x}{9}$ | D. | $\frac{x}{7}$-3=$\frac{x}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com