Question

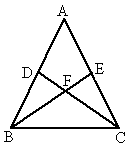
(2007，辽宁省大连市，16)如图，在△ABC中，AB=AC，点D、E分别是AB、AC的中点，点F是BE、CD的交点．请写出图中两组全等的三角形，并选出其中一组加以证明．

(要求：写出证明过程中的重要依据)

Answer 1

答案：略
解析：

解：△ABE≌△ACD，△BCD≌△CBE或△BFD≌△CFE(写出两个即可)． (1)选△ABE≌△ACD． 证明：∵点D、E分别是AB、AC的中点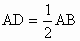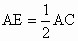， ∴，． 又∵AB=AC，∴AD=AE． 在△ABE和△ACD中， ∴△ABE≌△ACD(SAS)． (2)选△BCD≌△CBE． 证明：∵AB=AC， ∴∠ABC=∠ACB(等边对等角)． ∵点D、E分别是AB、AC的中点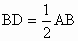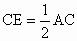，∴，． ∴． 在△BCD和△CBE中， ∴△BCD≌△CBE(SAS)． (3)选△BFD≌△CFE． 方法一： 证明：∵点D、E分别是AB、AC的中点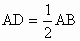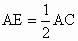， ∴，． 又∵AB=AC，∴AD=AE． 在△ABE和△ACD中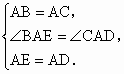 ∴△ABE≌△ACD(SAS)． ∴∠ABE=∠ACD(全等三角形对应角相等)． ∵点D、E分别是AB、AC的中点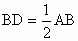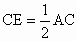， ∴，． ∵AB=AC，∴BD=CE． 在△BFD和△CFE中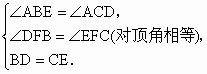， ∴△BFD≌△CFE(AAS)． 方法二： 证明：∵AB=AC， ∴∠ABC=∠ACB(等边对等角)． ∵点D、E分别是AB、AC的中点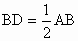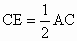， ∴，． ∴BD=CE． 在△BCD和△CBE中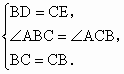， ∴△BCD≌△CBE(SAS)． ∴∠BDC=∠CEB(全等三角形对应角相等)． 在△BFD和△CFE中， ∴△BFD≌△CFE(AAS)．