
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC-CF=2HE;⑤AB=HF,其中正确的有( )
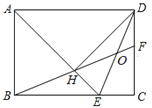
A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①②③⑤
【答案】B
【解析】试题解析:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE=![]() AB,
AB,
∵AD=![]() AB,
AB,
∴AE=AD,
在△ABE和△AHD中,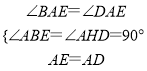 ,
,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠CED=180°-45°-67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵∠AHB=![]() (180°-45°)=67.5°,∠OHE=∠AHB(对顶角相等),
(180°-45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=∠AED,
∴OE=OH,
∵∠DOH=90°-67.5°=22.5°,∠ODH=67.5°-45°=22.5°,
∴∠DOH=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°-67.5°=22.5°,
∴∠EBH=∠OHD,
又∵BE=DH,∠AEB=∠HDF=45°
在△BEH和△HDF中
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
由上述①、②、③可得CD=BE、DF=EH=CE,CF=CD-DF,
∴BC-CF=(CD+HE)-(CD-HE)=2HE,所以④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④.
故选B.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(![]() )写出扇形图中
)写出扇形图中![]() __________
__________![]() ,并补全条形图.
,并补全条形图.
(![]() )在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
)在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
(![]() )该区体育中考选报引体向上的男生共有
)该区体育中考选报引体向上的男生共有![]() 人,如果体育中考引体向上达
人,如果体育中考引体向上达![]() 个以上(含
个以上(含![]() 个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列的推理过程补充完整,并在括号里填上推理的依据:
如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.
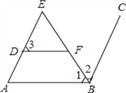
试说明:DF∥AB
解:因为BE是∠ABC的角平分线
所以 (角平分线的定义)
又因为∠E=∠1(已知)
所以∠E=∠2( )
所以 ( )
所以∠A+∠ABC=180°( )
又因为∠3+∠ABC=180°(已知)
所以 ( )
所以DF∥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数及方差如下表所示,如果要选出一个成绩好且状态稳定的组去参赛,那么应选的组是__________.
甲 | 乙 | 丙 | 丁 | |
平均数 | 7 | 8 | 8 | 7 |
方差 | 1 | 1.2 | 1 | 1.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
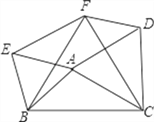
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF。
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足_____________________时,四边形AEFD是菱形。(无需证明)
②△ABC满足_______________________时,四边形AEFD是矩形。(无需证明)
③△ABC满足_______________________时,四边形AEFD是正方形。(无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
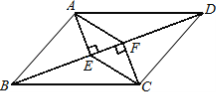
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com