
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

科目:初中数学 来源: 题型:
【题目】(1)如图1,在AB直线一侧C、D两点,在AB上找一点P,使C、D、P三点组成的三角形的周长最短,找出此点并说明理由.
(2)如图2,在∠AOB内部有一点P,是否在OA、OB上分别存在点E、F,使得E、F、P三点组成的三角形的周长最短,找出E、F两点,并说明理由.
(3)如图3,在∠AOB内部有两点M、N,是否在OA、OB上分别存在点E、F,使得E、F、M、N,四点组成的四边形的周长最短,找出E、F两点,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)15﹣(﹣8)+(﹣20)﹣12
(2)2×(﹣3)2﹣4×(﹣3)+15
(3)(﹣![]() )2+|﹣2|3﹣
)2+|﹣2|3﹣![]()
(4)﹣20+(﹣2)2﹣32+|﹣10|
(5)﹣22![]() ×
×![]() 2
2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡把果树林分为两部分,左地块用新技术管理,右地块用老方法管理,管理成本相同,她在左、右两地块上各随机选取20棵果树,按产品分成甲、乙、丙、丁四个等级(数据分组包括左端点不包括右端点),并制作如下两幅不完整的统计图: 
(1)补齐左地块统计图,求右地块乙级所对应的圆心角的度数;
(2)比较两地块的产量水平,并说明试验结果;
(3)在左地块随机抽查一棵果树,求该果树产量为乙级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4
∵(y+2)2≥0
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)求代数式m2+m+4的最小值;
(2)求代数式4﹣x2+2x的最大值;
(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)5m-7n-8p+5n-9m-p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5.
【答案】(1)-4m-2n-9p;(2)3x16
【解析】
(1)先移项,再合并同类项;
(2)原式利用幂的乘方、同底数幂的乘法和除法法则计算,再合并即可得到结果.
(1)5m-7n-8p+5n-9m-p=5m-9m-7n+5n-8p-p=-4m-2n-9p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5=- x4x5x7+5x16-x21÷x5=- x16 +5x16-x16=3x16
【点睛】
此题考查了幂的乘方、同底数幂的乘法、除法法则计算以及合并同类项,熟练掌握整式运算的有关法则是解答此题的关键.
【题型】解答题
【结束】
21
【题目】解方程:![]() (x-2)-
(x-2)-![]() (4x-1)=4.
(4x-1)=4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a+b=5,ab=-2,求代数式(6a-3b-2ab)-(a-8b-ab)的值;
(2)已知2x-y-4=0,求9x27y÷81y的值.
【答案】(1)27;(2)81.
【解析】
(1)运用整式的加减运算顺序先去括号,再合并同类项,根据乘法的分配律将5a+5b变形为5(a+b),最后代入求值即可;
(2)根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得答案.
(1)原式=6a-3b-2ab-a+8b+ab=5a+5b-ab=5(a+b)-ab,
当a+b=5,ab=-2时,
原式=5×5-(-2)=27;
(2)9x27y÷81y=32x33y÷34y=32x-y,
由2x-y-4=0,得2x-y=4,
故原式=34=81.
【点睛】
本题考查了幂的乘方,同底数幂的乘法,整式的混合运算和求值的应用,用了整体代入思想.
【题型】解答题
【结束】
23
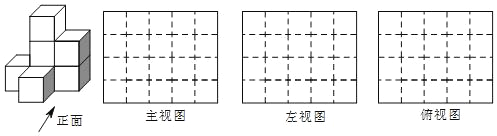
【题目】根据要求完成下列题目:
(1)图中有_____块小正方体;
(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图;
(3)用小正方体搭一几何体,使得它的俯视图和左视图与你在图方格中所画的图一致,若这样的几何体最少要m个小正方体,最多要n个小正方体,则m+n的值为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF. 
(1)证明:EF=CF;
(2)当 ![]() 时,求EF的长.
时,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com