
| 3 |
| 3 |
| ||
| 3 |
|
| 1 |
| 2 |
| BD2-DF2 |
| 3 |
| 3 |
| 3 |



科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
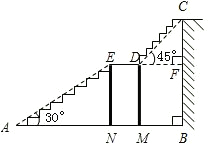 每平方米120元的地毯,求用地毯铺满整个楼梯共需要花费多少元钱?(结果精确到1元)
每平方米120元的地毯,求用地毯铺满整个楼梯共需要花费多少元钱?(结果精确到1元)查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
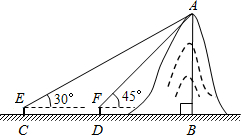 AB.(精确到1m,
AB.(精确到1m,| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
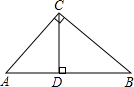
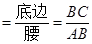 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:如图②,已知sinA
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:如图②,已知sinA ,其中∠A为锐角,试求sadA的值。
,其中∠A为锐角,试求sadA的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com