
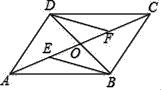
【题目】如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)求证:四边形DEBF是平行四边形;
(3)若OD=OE=OF,则四边形DEBF是什么特殊的四边形,请证明.
【答案】见解析
【解析】整体分析:
(1)用ASA证明△BOE≌△DOF;(2)连接DE、BF,用对角线互相平分的四边形是平行四边形证明;(3)四边形DEBF是平行四边形,且对角线相等.
(1)证明:∵DF∥BE,
∴∠DFE=∠BEO,
在△BOE和△DOF中,
∠DFE=∠BEO,OF=OE,∠DOF=∠EOB,
∴△BOE≌△DOF.
(2)证明:连接DE、BF.
∵△BOE≌△DOF,
∴OD=OB,∵OE=OF,
∴四边形DEBF是平行四边形.

(3)若OD=OE=OF,则四边形DEBF是矩形.
理由:∵OD=OE=OF=OB,
∴BD=EF,
∵四边形DEBF是平行四边形,
∴四边形DEBF是矩形.


科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的周长为20 cm,两条对角线AC,BD相交于点O,过点O作AC的垂线EF,分别交两边AD,BC于点E,F(不与顶点重合),则以下关于△CDE与△ABF判断完全正确的一项为( )
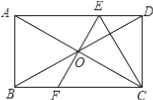
A. △CDE与△ABF的周长都等于10 cm,但面积不一定相等
B. △CDE与△ABF全等,且周长都为10 cm
C. △CDE与△ABF全等,且周长都为5 cm
D. △CDE与△ABF全等,但它们的周长和面积都不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,求△AED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个完全相同的大长方形,长为a,各放入四个完全一样的小长方形后,得到图(1)、图(2),那么图(1)阴影部分的周长与图(2)阴影部分的周长的差是( )(用含a的代数式表示)

A. ![]() a B.
a B. ![]() a C. a D.
a C. a D. ![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,EA是⊙O的切线.若∠EAC=120°,则∠ABC的度数是( ) 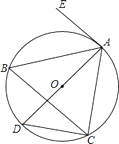
A.80°
B.70°
C.60°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y= ![]() x2﹣
x2﹣ ![]() x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
x﹣3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进A.B两种商品共160件,其进价和售价如表:
A | B | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
(1)当A.B两种商品分别购进多少件时,商店计划售完这批商品后能获利1100元;
(2)若商店计划购进A种商品不少于66件,且销售完这批商品后获利多于1260元,请你帮该商店老板预算有几种购货方案?获利最大是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com