
 如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( )
如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( )| A. | 12cm | B. | 16cm | C. | 20cm | D. | 28cm |
分析 利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,那么由折叠可得HF的长即为边AD的长.
解答  解:∵∠HEM=∠AEH,∠BEF=∠FEM,
解:∵∠HEM=∠AEH,∠BEF=∠FEM,
∴∠HEF=∠HEM+∠FEM=$\frac{1}{2}$×180°=90°,
同理可得:∠EHG=∠HGF=90°,
∴四边形EFGH为矩形.
∴EH=FG,EH∥FG,
∴∠EHF=∠HFG,
∵∠AHE=∠EHF,∠CFG=∠HFG,
∴∠AHE=∠CFG,
∵∠A=∠C,
∴△AHE≌△CFG,
∴AH=CF,
∴AH=CF=FP,
∵HD=HP,
∴AD=AH+HD=PF+HP=HF,
∵HF=$\sqrt{E{H}^{2}+E{F}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
∴AD=20cm,
故选C.
点评 本题是翻折变换问题,考查了学生对翻转、折叠矩形、三角形等知识的掌握情况,要熟知折叠前后图形的形状和大小不变,对应边和对应角相等;利用翻折的性质将相等的边转化为同一线段上,并利用勾股定理求出该线段的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,直径为1个单位长度的圆上一点A在数轴上的坐标为-1,该圆沿数轴向右滚动2014周,A点到达位置A′处,则A′的坐标为2014π-1.
如图,直径为1个单位长度的圆上一点A在数轴上的坐标为-1,该圆沿数轴向右滚动2014周,A点到达位置A′处,则A′的坐标为2014π-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
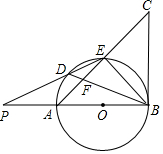 如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
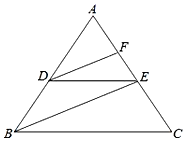 阅读下面的解题过程,并在横线上补全推理过程或依据.
阅读下面的解题过程,并在横线上补全推理过程或依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
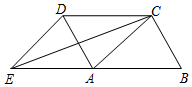 如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是( )
如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为菱形的是( )| A. | AB=AD | B. | AB=ED | C. | CD=AE | D. | EC=AD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com