
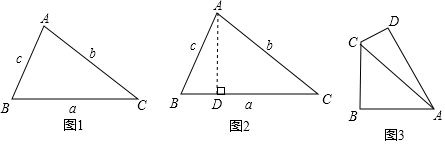
���� �������Ǻ����Ķ���õ�sinB=$\frac{AD}{AB}$��cosB=$\frac{BD}{AB}$�����ǵõ����ۣ���������õ�����ʽ�����ɣ���ͼ3��ʾ���ӳ�BC��AD����E����ֱ�������μ��ɵõ����ۣ�
��� �⣺��sinB=$\frac{AD}{AB}$��cosB=$\frac{BD}{AB}$��
��AD=AB•sinB=c•sinB��BD=AB•cosB=c•cosB��
CD=BC-BD=a-c•cosB��
���b2=AD2+DC2�T��c•sinB��2+��a-c•cosB��2
=c2sin2B+a2+c2cos2B+2ac•cosB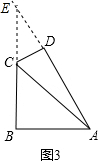
=c2��sin2B+cos2B��+a2-2ac•cosB
=a2+c2-2ac•cosB��
��ͼ3��ʾ���ӳ�BC��AD����E��
�ߡ�B=90�㣬��BAD=60�㣬AB=4��
��AE=2AB=8����E=30�㣬
��AD=5��
��DE=3��
�ߡ�ADC=��CDE=90�㣬
��CE=2$\sqrt{3}$��
��AC2=CE2+AE2-2CE•AEcos30��=12+64-2��$2\sqrt{3}$��8��$\frac{\sqrt{3}}{2}$=28��
��AC=2$\sqrt{7}$��
�ʴ��ǣ�c•sinB��c•cosB��a2+c2-2ac•cosB��
���� ���⿼���˽�ֱ�������Σ����Ҷ�������ȷ�����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����һ�������Խ�ĺ��ӣ��������·�������AOB�Ľ�ƽ���ߣ�
С����һ�������Խ�ĺ��ӣ��������·�������AOB�Ľ�ƽ���ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
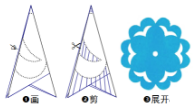 ��ֽ���й����ϵĺ��崫ͳ�������֮һ��������������ֽ�ļ����̣�չ����ļ�ֽͼ���ӶԳ������жϣ�������
��ֽ���й����ϵĺ��崫ͳ�������֮һ��������������ֽ�ļ����̣�չ����ļ�ֽͼ���ӶԳ������жϣ�������| A�� | ����Գ�ͼ�ε��������ĶԳ�ͼ�� | |
| B�� | �����ĶԳ�ͼ�ε�������Գ�ͼ�� | |
| C�� | ������Գ�ͼ��Ҳ�����ĶԳ�ͼ�� | |
| D�� | �Ȳ�����Գ�ͼ��Ҳ�������ĶԳ�ͼ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
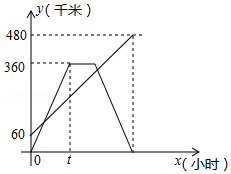 �ס��������ֱ�����480km��A��B����������У��ҳ��ȼ׳��ȳ���1Сʱ�����Ը��Ե��ٶ�������ʻ��;��C�أ��׳�����C��ͣ��1Сʱ�������°�ԭ·ԭ�ٷ���A�أ��ҳ���B��ֱ��A�أ�����ͬʱ����A�أ��ס�����������Գ����ص�·��y��ǧ�ף���׳��������õ�ʱ��x��Сʱ���Ĺ�ϵ��ͼ�����ͼ����Ϣ����������⣺
�ס��������ֱ�����480km��A��B����������У��ҳ��ȼ׳��ȳ���1Сʱ�����Ը��Ե��ٶ�������ʻ��;��C�أ��׳�����C��ͣ��1Сʱ�������°�ԭ·ԭ�ٷ���A�أ��ҳ���B��ֱ��A�أ�����ͬʱ����A�أ��ס�����������Գ����ص�·��y��ǧ�ף���׳��������õ�ʱ��x��Сʱ���Ĺ�ϵ��ͼ�����ͼ����Ϣ����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com