

分析 (1)利用等腰直角三角形的性质以及三角形中位线定理,得出得出MN与EC的数量关系;
(2)先连接EM并延长至点F,使MF=EM,判定△EDM≌△FBM,进而运用SAS判定△EAC≌△FBC,即可得出FC=EC,再利用三角形中位线定理,得出MN与FC的数量关系,进而得出结论;
(3)先延长DN到G,使DN=GN,连接CG,延长DE、CA交于点K,再通过判定△EDN≌△CGN和△CAE≌△BCG,进而得出结论.
解答 解:(1)MN与EC的数量关系为MN=$\frac{1}{2}$EC,
证明:∵点M,N分别是DB,EC的中点,
∴MN=$\frac{1}{2}$EB,
∵等腰Rt△AED,∠AED=∠ACB=90°,
∴∠B=∠ACE=45°,
∴∠BCE=90°-45°=45°,
∴BE=CE,
∴MN=$\frac{1}{2}$EC;
(2)成立
证明:如图2,连接EM并延长至点F,使MF=EM,连接CF,BF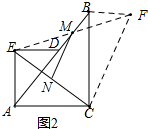 ,
,
在△EDM和△FBM中,
$\left\{\begin{array}{l}{DM=BM}\\{∠EMD=∠FMB}\\{EM=FM}\end{array}\right.$,
∴△EDM≌△FBM(SAS),
∴BF=DE=AE,∠FBM=∠EDM,
∵△AED为等腰直角三角形,∠AED=∠ACB=90°,
∴∠BAC=∠ABC=45°,
∴△ABC是等腰直角三角形,
∴∠EAD=∠EDA=∠BAC=∠ABC=45°,AC=BC,
∴∠FBM=∠EDM=135°,
∴∠FBC=∠EAC=90°,
在△EAC和△FBC中,
$\left\{\begin{array}{l}{AE=BF}\\{∠EAC=∠FBC}\\{AC=BC}\end{array}\right.$,
∴△EAC≌△FBC(SAS),
∴FC=EC,
又∵点M,N分别是EF,EC的中点,
∴MN=$\frac{1}{2}$FC,
∴MN=$\frac{1}{2}$EC;
(3)MN与EC的位置关系为:MN⊥EC,数量关系为:MN=$\frac{1}{2}$EC.
点评 本题主要考查了几何变换变换中的旋转变换,解决问题的关键是掌握三角形中位线定理以及全等三角形的判定和性质.解决此类试题时,需要灵活运用等腰直角三角形的性质,并且需要经过中点作辅助线构造全等三角形.


科目:初中数学 来源: 题型:填空题
 如图,在菱形ABCD中,E是BC边上的点,AE交BD于点F,若EC=2BE,则$\frac{BF}{FD}$的值是$\frac{1}{3}$.
如图,在菱形ABCD中,E是BC边上的点,AE交BD于点F,若EC=2BE,则$\frac{BF}{FD}$的值是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
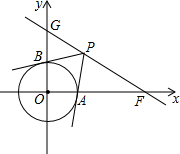 如图,在平面直角坐标系中,O为坐标原点,已知点F(2$\sqrt{3}$,0),直角GF交y轴正半轴于点G,且∠GFO=30°.
如图,在平面直角坐标系中,O为坐标原点,已知点F(2$\sqrt{3}$,0),直角GF交y轴正半轴于点G,且∠GFO=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
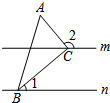 如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则
如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且AC⊥BC,若∠1=40°,则| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
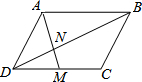 如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N,若已知S△DMN=3,那么S△BAN等于( )
如图,在平行四边形ABCD中,如果点M为CD的中点,AM与BD相交于点N,若已知S△DMN=3,那么S△BAN等于( )| A. | 6 | B. | 9 | C. | 12 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月均用水量 | 2≤x<3 | 3≤x<4 | 4≤x<5 | 5≤x<6 | 6≤x<7 | 7≤x<8 | 8≤x<9 |
| 频数 | 2 | 12 | ① | 10 | ② | 3 | 2 |
| 百分比 | 4% | 24% | 30% | 20% | ③ | 6% | 4% |
| a1 | a2 | b1 | b2 | b3 | |
| a1 | |||||
| a2 | |||||
| b1 | |||||
| b2 | |||||
| b3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com