
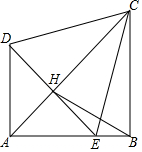
 将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:
将两个等腰Rt△ADE,Rt△ABC(其中∠DAE=∠ABC=90°,AB=BC,AD=AE)如图放置在一起,点E在AB上,AC与DE交于点H,连接BH、CE,且∠BCE=15°,下列结论:| A. | 只有①② | B. | 只有③④ | C. | 只有①②④ | D. | ①②③④ |
分析 利用等腰直角三角形的性质得出∠DAC=∠BAC即可判断出①正确;再用等腰直角三角形的内角的关系即可得出∠DCE=60°,即可得出②正确,判断出∠BCD=75°=∠BEC即可判断出③正确,设出AH=x,利用等腰直角三角形和等边三角形的性质即可得出CH,EH,AB,BE最后用三角形的面积公式即可得出④正确.
解答 解:∵△ABC和△ADE是等腰直角三角形,
∴∠BAC=∠ACB=45°,∠DAE=90°,
∴∠DAC=∠BAC=45°,
∵AD=AE,
∴AC垂直平分DE,∴①正确,
∵AC垂直平分DE,
∴DC=EC,∠DAC=∠EAC,
∵∠BCE=15°,
∴∠ACE=30°,
∴∠DCE=2∠ACE=60°,
∴△CDE是等边三角形,∴②正确;
∵∠DCE=60°,∠BCE=15°,
∴∠BCD=75°,
∵∠BEC=90°-15°=75°,
∴∠BCD=∠BEC,
在Rt△BCE中,tan∠BEC=$\frac{BC}{BE}$=$\frac{AB}{BE}$,
∴tan∠BCD=$\frac{AB}{BE}$,∴③正确;
设AH=x,
在Rt△AEH中,HE=AH=x,AE=$\sqrt{2}$x,
在Rt△CEH中,∠ECH=30°,
∴CH=$\sqrt{3}$EH=$\sqrt{3}$x,CE=2HE=2x,
∴AC=AH+CH=($\sqrt{3}$+1)x,
在Rt△ABC中,BC=AB=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1)x=$\frac{\sqrt{6}+\sqrt{2}}{2}$x,
∴BE=AB-AE=$\frac{\sqrt{6}-\sqrt{2}}{2}$x,
∴S△BCE=$\frac{1}{2}$BE•BC=$\frac{1}{2}$×$\frac{\sqrt{6}-\sqrt{2}}{2}$x•$\frac{\sqrt{6}+\sqrt{2}}{2}$x=$\frac{1}{2}$x2
S△EHC=$\frac{1}{2}$EH•CH=$\frac{1}{2}$x•$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2,∴$\frac{{S}_{△BCE}}{{S}_{△EHC}}=\frac{\frac{1}{2}{x}^{2}}{\frac{\sqrt{3}}{2}{x}^{2}}$=$\frac{\sqrt{3}}{3}$,∴④正确,
即:正确的有①②③④,
故选D.
点评 此题是三角形综合题,主要考查了等腰直角三角形的性质,等边三角形的性质和判定,含30°的直角三角形的性质,线段的垂直平分线的性质和判定,勾股定理,解本题的关键是灵活运用特殊三角形的性质;是一道基础题目.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com